
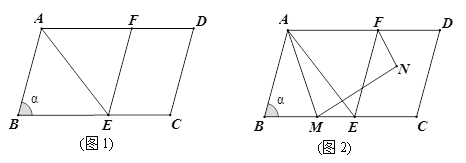
【题目】如图1,在□ABCD中,AB=6,∠B= ![]() (60°<
(60°<![]() ≤90°). 点E在BC上,连接AE,把△ABE沿AE折叠,使点B与AD上的点F重合,连接EF.
≤90°). 点E在BC上,连接AE,把△ABE沿AE折叠,使点B与AD上的点F重合,连接EF.
(1)求证:四边形ABEF是菱形;
(2)如图2,点M是BC上的动点,连接AM,把线段AM绕点M顺时针旋转![]() 得到线段MN,连接FN,求FN的最小值(用含
得到线段MN,连接FN,求FN的最小值(用含![]() 的代数式表示).
的代数式表示).
【答案】(1)详见解析;(2)FE·sin(![]()
![]() -90°)
-90°)
【解析】
(1)由四边形ABCD是平行四边形得AF∥BE,所以∠FAE=∠BEA,由折叠的性质得∠BAE=∠FAE,∠BEA=∠FEA,所以∠BAE=∠FEA,故有AB∥FE,因此四边形ABEF是平行四边形,又BE=EF,因此可得结论;
(2)根据点M在线段BE上和EC上两种情况证明∠ENG=90°-![]()
![]() ,利用菱形的性质得到∠FEN=
,利用菱形的性质得到∠FEN=![]()
![]() -90°,再根据垂线段最短,求出FN的最小值即可.
-90°,再根据垂线段最短,求出FN的最小值即可.
(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠FAE=∠BEA,
由折叠的性质得∠BAE=∠FAE,∠BEA=∠FEA, BE=EF,
∴∠BAE=∠FEA,
∴AB∥FE,
∴四边形ABEF是平行四边形,
又BE=EF,
∴四边形ABEF是菱形;
(2)①如图1,当点M在线段BE上时,在射线MC上取点G,使MG=AB,连接GN、EN.
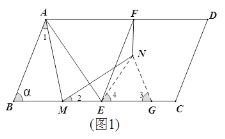
∵∠AMN=∠B=![]() ,∠AMN+∠2=∠1+∠B
,∠AMN+∠2=∠1+∠B
∴∠1=∠2
又AM=NM,AB=MG
∴△ABM≌△MGN
∴∠B=∠3,NG=BM
∵MG=AB=BE
∴EG=AB=NG
∴∠4=∠ENG=![]() (180°-
(180°-![]() )=90°-
)=90°-![]()
![]()
又在菱形ABEF中,AB∥EF
∴∠FEC=∠B=![]()
∴∠FEN=∠FEC-∠4=![]() - (90°-
- (90°-![]()
![]() )=
)=![]()
![]() -90°
-90°
②如图2,当点M在线段EC上时,在BC延长线上截取MG=AB,连接GN、EN.
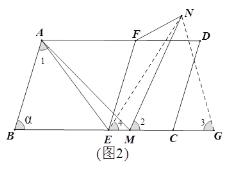
同理可得:∠FEN=∠FEC-∠4=![]() - (90°-
- (90°-![]()
![]() )=
)=![]()
![]() -90°
-90°
综上所述,∠FEN=![]()
![]() -90°
-90°
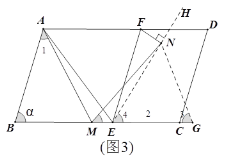
∴当点M在BC上运动时,点N在射线EH上运动(如图3)
当FN⊥EH时,FN最小,其最小值为FE·sin(![]()
![]() -90°)
-90°)


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.
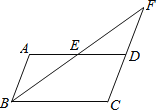
(1)证明:FD=AB;(2)当平行四边形ABCD的面积为8时,求△FED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
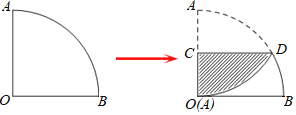
【题目】如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为( )
A. 6π﹣![]() B. 6π﹣9
B. 6π﹣9![]() C. 12π﹣
C. 12π﹣![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
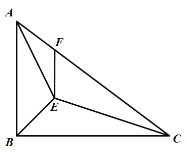
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点E是△ABC的内心,过点E作EF∥AB交AC于点F,则EF的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,对角线AC、BD相交于点O,点E是BC的中点,AE交BD于点F,BH⊥AE于点G,连接OG,则下列结论中①OF=OH,②△AOF∽△BGF,③tan∠GOH=2,④FG+CH=![]() GO,正确的个数是( )
GO,正确的个数是( )
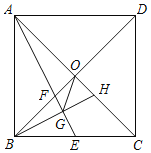
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
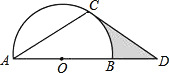
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以“学习朱子文化,弘扬理学思想”为主题的读书月活动,并向学生征集读后感,学校将收到的读后感篇数按年级进行统计,绘制了以下两幅统计图(不完整).
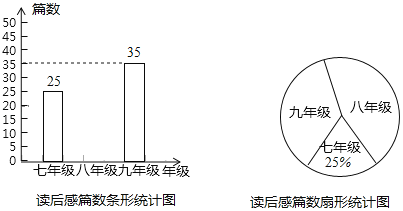
据图中提供的信息完成以下问题
(1)扇形统计图中“八年级”对应的圆心角是 °,并补全条形统计图;
(2)经过评审,全校有4篇读后感荣获特等奖,其中有一篇来自七年级,学校准备从特等奖读后感中任选两篇在校广播电台上播出,请利用画树状图或列表的方法求出七年级特等奖读后感被校广播电台播出的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
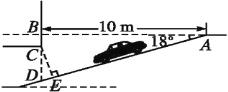
【题目】.某商场为缓解“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5 m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说得对?请你判断并计算出正确的结果.(结果精确到0.1 m,参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.325)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD表示该产品每千克生产成本y1(单位:元)与产量x(单位:kg)之间的函数关系;线段CD表示每千克的销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
(1)请解释图中点D的横坐标、纵坐标的实际意义.
(2)求线段AB所表示的y1与x之间的函数表达式.
(3)当0≤x≤90时,销售该产品获得的利润与产量的关系式是 ;当90≤x≤130时,销售该产品获得的利润与产量的关系式是 ;总之,当产量为 kg时,获得的利润最大,最大利润是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com