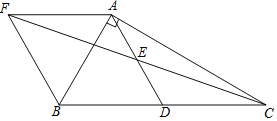
【题目】如图，在
中，
，
，
，点D、E分别是BC、AD的中点，
交CE的延长线于点F，则四边形AFBD的面积为______．
科目：初中数学 来源： 题型：
【题目】已知抛物线y=x2﹣2x+a（a＜0）与y轴相交于点A，顶点为M．直线y=
x﹣a分别与x轴，y轴相交于B，C两点，并且与直线AM相交于点N．
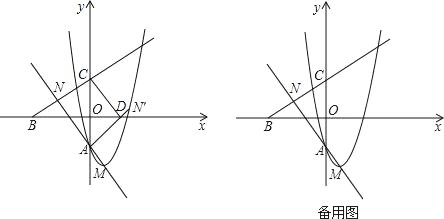
（1）试用含a的代数式分别表示点M与N的坐标；
（2）如图，将△NAC沿y轴翻折，若点N的对应点N′恰好落在抛物线上，AN′与x轴交于点D，连接CD，求a的值和四边形ADCN的面积；
（3）在抛物线y=x2﹣2x+a（a＜0）上是否存在一点P，使得以P，A，C，N为顶点的四边形是平行四边形？若存在，求出P点的坐标；若不存在，试说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某书店老板去图书批发市场购买某种图书，第一次用1200元购书若干本，并按该书定价7元出售，很快售完．由于该书畅销，第二次购书时，每本书的批发价已比第一次提高了20%，他用1500元所购该书的数量比第一次多10本，当按定价售出200本时，出现滞销，便以定价的4折售完剩余的书．
（1）第一次购书的进价是多少元？
（2）试问该老板这两次售书总体上是赔钱了，还是赚钱了（不考虑其他因素）？若赔钱，赔多少；若赚钱，赚多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
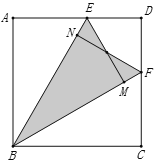
【题目】如图，正方形ABCD的边长为
，点E、F分别为边AD、CD上一点，将正方形分别沿BE、BF折叠，点A的对应点M恰好落在BF上，点C的对应点N恰好落在BE上，则图中阴影部分的面积为_________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】读下列因式分解的过程，再回答所提出的问题：
1 x x(1 x) x(1 x)2
(1 x)[1 x x(1 x)]
(1 x)2 (1 x)
(1 x)3
（1）上述分解因式的方法是 ，共应用了 次．
（2）若分解1 x x(1 x) x(1 x)2 … x(1 x)2018，则需应用上述方法 次，结果是 ．
（3）分解因式：1 x x(1 x) x(1 x)2… x(1 x)n
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，D是BA延长线上的一点，点E是AC的中点.
(1)实践与操作：利用尺规按下列要求作图，并在图中标明相应字母(保留作图痕迹，不写作法).
①作∠DAC的平分线AM；
②连接BE并延长交AM于点F；
③连接FC.
(2)猜想与证明：猜想四边形ABCF的形状，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义:若a+b=2，则称a与b是关于1的平衡数.
(1)直接填写:①3与_ 是关于1的平衡数: :
②1-x与________是关于 1的平衡数(用含x的代数式表示);
(2)若
，
,先化简a. b,再判断a与b是否是关于1的平衡数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①所示是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均分成四个小长方
形，然后按图②的方式拼成一个正方形。
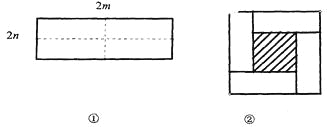
(1)你认为图②中的阴影部分的正方形的边长等于_________________.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积。
方法①_________________________________________________________.
方法②_________________________________________________________.
(3)观察图②，你能写出
，
，mn这三个代数式间的等量关系吗?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在△ABC和△DBC中，∠ACB=∠DBC=90°，点E是BC的中点，EF⊥AB，垂足为F，且AB=DE．
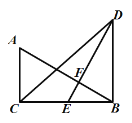
（1）求证：△BCD是等腰直角三角形；
（2）若BD=8厘米，求AC的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
