练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

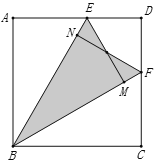
    【题目】如图，正方形ABCD的边长为 ，点E、F分别为边AD、CD上一点，将正方形分别沿BE、BF折叠，点A的对应点M恰好落在BF上，点C的对应点N恰好落在BE上，则图中阴影部分的面积为_________．

    【答案】

    【解析】分析：设NE＝x，由对称的性质和勾股定理，用x分别表示出ON，OE，OM，在直角△OEN中用勾股定理列方程求x，则可求出△OBE的面积.

    详解：连接BO.

    ∠ABE＝∠EBF＝∠FBC＝30°，AE＝1＝EM，BE＝2AE＝2.

    ∠BNF＝90°，∠NEO＝60°，∠EON＝30°，

    设EN＝x，则EO＝2x，ON＝x＝OM，

    ∴OE＋OM＝2x＋x＝(2＋)x＝1.∴x＝＝2－.

    ∴ON＝x＝(2－)＝2－3.

    ∴S＝2S△BOE＝2×(×BE×ON)＝2×[×2×(2－3)]＝4－6.

    故答案为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】直线AB，CD交于点O，将一个三角板的直角顶点放置于点O处，使其两条直角边OE，OF，分别位于OC的两侧．若OC平分∠BOF，OE平分∠COB．

    （1）求∠BOE的度数；

    （2）写出图中∠BOE的补角，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

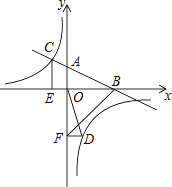
    【题目】如图，在平面直角坐标系中，直线AB与x轴交于点B，与y轴交于点A，与反比例函数的图象在第二象限交于点C，CE⊥x轴，垂足为点E，，OB=4，OE=2.

    （1）求反比例函数的解析式；

    （2）若点D是反比例函数图象在第四象限上的点，过点D作DF⊥y轴，垂足为点F连接OD、BF，如果，求点D的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了保护环境，某化工厂一期工程完成后购买了3台甲型和2台乙型污水处理设备，共花费资金54万元，且每台乙型设备的价格是每台甲型设备价格的75%，实际运行中发现，每台甲型设备每月能处理污水200吨，每台乙型设备每月能处理污水160吨，且每年用于每台甲型设备的各种维护费和电费为1万元，每年用于每台乙型设备的各种维护费和电费为1.5万元.今年该厂二期工程即将完成，产生的污水将大大增加，于是该厂决定再购买甲、乙两型设备共8台用于二期工程的污水处理，预算本次购买资金不超过84万元，预计二期工程完成后每月将产生不少于1300吨污水.

    （1）请你计算每台甲型设备和每台乙型设备的价格各是多少元？

    （2）请你求出用于二期工程的污水处理设备的所有购买方案；

    （3）若两种设备的使用年限都为10年，请你说明在（2）的所有方案中，哪种购买方案的总费用最少？（总费用＝设备购买费＋各种维护费和电费）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

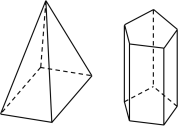
    【题目】（1）下面两个立体图形的名称是：__________，__________

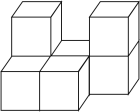
    （2）一个立体图形的三视图如下图所示，这个立体图形的名称是__________

    （3）画出下面立体图形的主视图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在“爱我永州”中学生演讲比赛中，五位评委分别给甲、乙两位选手的评分如下：

    甲：8、7、9、8、8

    乙：7、9、6、9、9

    则下列说法中错误的是（ ）

    A．甲、乙得分的平均数都是8

    B．甲得分的众数是8，乙得分的众数是9

    C．甲得分的中位数是9，乙得分的中位数是6

    D．甲得分的方差比乙得分的方差小

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，，，点D、E分别是BC、AD的中点，交CE的延长线于点F，则四边形AFBD的面积为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知: ，.

    (1)当x=1和-1时，分别求P，Q的值；

    (2)当x=19时，P的值为a, Q的值为b，当x=-19时，分别求P, Q的值(用含a，b的代数式表示)；

    (3)当x=m时，P, Q的值分别为c, d; 当x=-m时，P, Q的值分别为e, f,则在c，d, e, f四个有理数中，以下判断正确的是 (只要填序号即可).

    ①有两个相等的正数；②有两个互为相反数；③至多有两个正数；④至少有两个正数；⑤至多有一个负数；⑥至少有一个负数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】滴滴打车为市民的出行带来了很大的方便，小亮调查了若干市民一周内使用滴滴打车的时间t（单位：分），将获得的数据分成四组，绘制了如下统计图，请根据图中信息，解答下列问题：

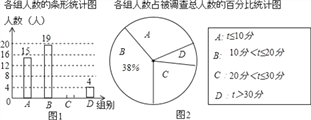
    （1）这次被调查的总人数是多少？

    （2）试求表示C组的扇形圆心角的度数，并补全条形统计图；

    （3）若全市的总人数为666万，试求全市一周内使用滴滴打车超过20分钟的人数大约有多少？

    查看答案和解析>>

    同步练习册答案