
【题目】直线AB,CD交于点O,将一个三角板的直角顶点放置于点O处,使其两条直角边OE,OF,分别位于OC的两侧.若OC平分∠BOF,OE平分∠COB.
(1)求∠BOE的度数;
(2)写出图中∠BOE的补角,并说明理由.

【答案】(1)30°;(2)∠BOE的补角有∠AOE和∠DOE.
【解析】
(1)根据OC平分∠BOF,OE平分∠COB.可得∠BOE=∠EOC=![]() ∠BOC,∠BOC=∠COF,进而得出,∠EOF=3∠BOE=90°,求出∠BOE;
∠BOC,∠BOC=∠COF,进而得出,∠EOF=3∠BOE=90°,求出∠BOE;
(2)根据平角和互补的意义,通过图形中可得∠BOE+∠AOE=180°,再根据等量代换得出∠BOE+∠DOE=180°,进而得出∠BOE的补角.
解:(1)∵OC平分∠BOF,OE平分∠COB.
∴∠BOE=∠EOC=![]() ∠BOC,∠BOC=∠COF,
∠BOC,∠BOC=∠COF,
∴∠COF=2∠BOE,
∴∠EOF=3∠BOE=90°,
∴∠BOE=30°,
(2)∵∠BOE+∠AOE=180°
∴∠BOE的补角为∠AOE;
∵∠EOC+∠DOE=180°,∠BOE=∠EOC,
∴∠BOE+∠DOE=180°,∴∠BOE的补角为∠DOE;
答:∠BOE的补角有∠AOE和∠DOE;


科目:初中数学 来源: 题型:
【题目】将一些相同的“○”按如图所示的规律依次摆放,观察每个“龟图”中的“○”的个数,若第n个“龟图”中有245个“○”,则n=( )

A. 14 B. 15 C. 16 D. 17
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林同学积极参加体育锻炼,天天坚持跑步,他每天以1000m为标准,超过的记作正数,不足的记作负数.下表是一周内小明跑步情况的记录(单位:m):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
跑步情况(m) | +420 | +460 | -100 | -210 | -330 | +200 | -240 |
(1)星期三小林跑了_____米
(2)小林在跑得最少的一天跑了______米?跑得最多的一天比最少的一天多跑了_____米?
(3)若小林跑步的平均速度为240米/分,求本周内小明用于跑步的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
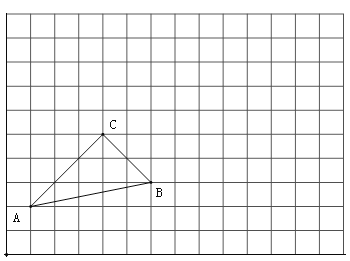
【题目】如图,△ABC是格点三角形(各顶点是网格线的交点), 每个小方格都是边长为1个单位长度的小正方形.
(1)将△ABC向右平移6个单位长度,画出平移后的△A1B1C1.
(2)将平移后的△A1B1C1绕点B1顺时针旋转90°,画出旋转后的△A2B1C2.
(3)将△ABC沿直线BC翻折,画出翻折后的△A3BC.
(4)试问△ABC能否经过一次旋转后与△A2B1C2重合,若能,请在图中用字母O表示旋转中心并写出旋转角的大小;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:在数轴上描出下列各组数:1与3, 2与-5, -4与-1
(1) 观察描在数轴上的每组数,说明表示每组数的两点之间的距离与这组数有何关系?
答 .
(2)若果a,b表示两个有理数,判断![]() ____
____ ![]() (填>,=或<)
(填>,=或<)
(3)当x为何值时:![]() 与
与![]() 的值相等。
的值相等。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数 a、b、c 在数轴上对应的点的位置,如图所示:① abc<0;② |a-b|+|b-c|=|a-c|;③ (a-b)(b-c)(c-a)>0;④ |a|<1-bc,以上四个结论正确的有( )个
![]()
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2x+a(a<0)与y轴相交于点A,顶点为M.直线y=![]() x﹣a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x﹣a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
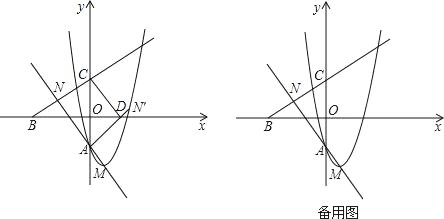
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x2﹣2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=mx2﹣(m+n)x+n(m<0)的图象与y轴正半轴交于A点.
(1)求证:该二次函数的图象与x轴必有两个交点;
(2)设该二次函数的图象与x轴的两个交点中右侧的交点为点B,若∠ABO=45°,将直线AB向下平移2个单位得到直线l,求直线l的解析式;
(3)在(2)的条件下,设M(p,q)为二次函数图象上的一个动点,当﹣3<p<0时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
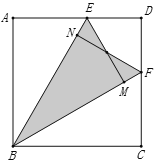
【题目】如图,正方形ABCD的边长为![]() ,点E、F分别为边AD、CD上一点,将正方形分别沿BE、BF折叠,点A的对应点M恰好落在BF上,点C的对应点N恰好落在BE上,则图中阴影部分的面积为_________.
,点E、F分别为边AD、CD上一点,将正方形分别沿BE、BF折叠,点A的对应点M恰好落在BF上,点C的对应点N恰好落在BE上,则图中阴影部分的面积为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com