
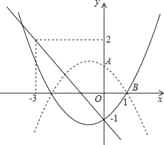
����Ŀ����ƽ��ֱ������ϵxOy�У����κ���y=mx2����m+n��x+n��m��0����ͼ����y�������ύ��A�㣮
��1����֤���ö��κ�����ͼ����x������������㣻
��2����ö��κ�����ͼ����x��������������Ҳ�Ľ���Ϊ��B������ABO=45������ֱ��AB����ƽ��2����λ�õ�ֱ��l����ֱ��l�Ľ���ʽ��
��3���ڣ�2���������£���M��p��q��Ϊ���κ���ͼ���ϵ�һ�����㣬����3��p��0ʱ����M����x��ĶԳƵ㶼��ֱ��l���·�����m��ȡֵ��Χ��
���𰸡���1���ö��κ�����ͼ����������������㣻��2��y=��x��1����3��m��ȡֵ��ΧΪ����![]() ��m��0��
��m��0��
�������������������1��ֱ�����ø����б�ʽ�������ȫƽ����ʽ������ķ��Ž����ó��𰸣�
��2���������B��A�����꣬�������ֱ��AB�Ľ���ʽ��������ƽ�ƹ��ɵó��𰸣�
��3�����ݵ���3��p��0ʱ����M����x��ĶԳƵ㶼��ֱ��l���·�����p=0ʱ��q=1����p=��3ʱ��q=12m+4�����ͼ���֪������12m+4����2�����ɵó�m��ȡֵ��Χ��
�����������1����mx2����m+n��x+n=0������=��m+n��2��4mn=��m��n��2��
�����κ���ͼ����y�������ύ��A�㣬��A��0��n������n��0��
����m��0����m��n��0�����=��m��n��2��0��
���ö��κ�����ͼ����������������㣻
��2����mx2����m+n��x+n=0����ã�x1=1��x2=![]() ���ɣ�1����
���ɣ�1����![]() ��0����B������Ϊ��1��0����
��0����B��������1��0����
������ABO=45����
����A��0��1������n=1��
������ֱ��AB�Ľ���ʽΪ��y=��x+1��
������ƽ��2����λ�ɵõ�ֱ��l��y=��x��1��
��3���ɣ�2���ö��κ����Ľ���ʽΪ��y=mx2����m+1��x+1��
��M��p��q�� Ϊ���κ���ͼ���ϵ�һ�����㣬
��q=mp2����m+1��p+1��
����M������ĶԳƵ�M��������Ϊ��p����q����
��M�����ڶ��κ���y=��m2+��m+1��x��1�ϣ�
������3��p��0ʱ����M����x��ĶԳƵ㶼��ֱ��l���·���
��p=0ʱ��q=1����p=��3ʱ��q=12m+4��
���ͼ���֪������12m+4����2����ã�m����![]() ��
��
��m��ȡֵ��ΧΪ����![]() ��m��0��
��m��0��


 ��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
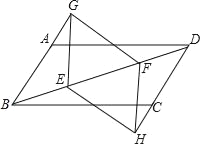
����Ŀ����ͼ����ABCD�У�E��F�ǶԽ���BD�ϵ����㣬BE��DF����G��H�ֱ���BA��DC���ӳ����ϣ���AG��CH������GE��EH��HF��FG��
��֤��(1)��BEG�ա�DFH��
(2)�ı���GEHF��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��AB��CD���ڵ�O����һ�����ǰ��ֱ�Ƕ�������ڵ�O����ʹ������ֱ�DZ�OE��OF���ֱ�λ��OC�����࣮��OCƽ�֡�BOF��OEƽ�֡�COB��
��1�����BOE�Ķ�����
��2��д��ͼ�С�BOE�IJ��ǣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
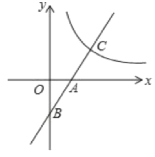
����Ŀ����ͼ,��֪һ�κ���y=2x2��ͼ����x,y��ֱ��ڵ�A,B,�뷴��������y=![]() (x>0)��ͼ���ڵ�C,��AB=AC,��k��ֵΪ()
(x>0)��ͼ���ڵ�C,��AB=AC,��k��ֵΪ()
A.5B.4C.3D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ���ڵ�һ���������ڵ�
��ͼ���ڵ�һ���������ڵ�![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ��
��![]() �Ḻ�����ϣ�
�Ḻ�����ϣ�![]() �����ı���
�����ı���![]() ��ƽ���ı��Σ���
��ƽ���ı��Σ���![]() ��������Ϊ
��������Ϊ![]() .
.
��1����÷�����������һ�κ����ı���ʽ��
��2������![]() ����
����![]() �������
�������
��3��ֱ��д������![]() �IJ���ʽ
�IJ���ʽ![]() �Ľ⼯.
�Ľ⼯.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ܵ��ֻ����»�����Ӱ�죬ij�꾭���ļ��ͺ��ֻ�������ۼ۱�ȥ��ÿ̨����500Ԫ�����������ͬ�������ֻ�����ôȥ�����۶�Ϊ8��Ԫ���������۶�ֻ��6��Ԫ��
��1��������ͺ��ֻ�ÿ̨�ۼ�Ϊ����Ԫ��
��2��Ϊ��������õ�ƻ��������ͺ��ֻ����ۣ���֪���ͺ��ֻ�ÿ̨����Ϊ1000Ԫ�����ͺ��ֻ�ÿ̨����Ϊ800Ԫ��Ԥ���ò�����1.84��Ԫ�Ҳ�����1.76��Ԫ���ʽ��������ֻ���20̨�������м��ֽ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
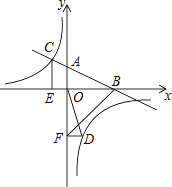
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ύ�ڵ�B����y�ύ�ڵ�A���뷴��������![]() ��ͼ���ڵڶ������ڵ�C��CE��x�ᣬ����Ϊ��E��
��ͼ���ڵڶ������ڵ�C��CE��x�ᣬ����Ϊ��E��![]() ��OB=4��OE=2.
��OB=4��OE=2.
��1�����������Ľ���ʽ��
��2������D�Ƿ���������ͼ���ڵ��������ϵĵ㣬����D��DF��y�ᣬ����Ϊ��F����OD��BF�����![]() �����D������.
�����D������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˱���������ij������һ�ڹ�����ɺ�����3̨���ͺ�2̨������ˮ�����豸���������ʽ�54��Ԫ����ÿ̨�����豸�ļ۸���ÿ̨�����豸�۸��75%��ʵ�������з��֣�ÿ̨�����豸ÿ���ܴ�����ˮ200�֣�ÿ̨�����豸ÿ���ܴ�����ˮ160�֣���ÿ������ÿ̨�����豸�ĸ���ά���Ѻ͵��Ϊ1��Ԫ��ÿ������ÿ̨�����豸�ĸ���ά���Ѻ͵��Ϊ1.5��Ԫ.����ó����ڹ��̼�����ɣ���������ˮ��������ӣ����Ǹó������ٹ���ס��������豸��8̨���ڶ��ڹ��̵���ˮ������Ԥ�㱾�ι����ʽ�������84��Ԫ��Ԥ�ƶ��ڹ�����ɺ�ÿ�½�����������1300����ˮ.
��1���������ÿ̨�����豸��ÿ̨�����豸�ļ۸���Ƕ���Ԫ��
��2������������ڶ��ڹ��̵���ˮ�����豸�����й�����
��3���������豸��ʹ������Ϊ10�꣬����˵���ڣ�2�������з����У����ֹ������ܷ������٣����ܷ��ã��豸����ѣ�����ά���Ѻ͵�ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪: ![]() ��
��![]() .
.
(1)��x=1��-1ʱ���ֱ���P��Q��ֵ��
(2)��x=19ʱ��P��ֵΪa, Q��ֵΪb����x=-19ʱ���ֱ���P, Q��ֵ(�ú�a��b�Ĵ���ʽ��ʾ)��
(3)��x=mʱ��P, Q��ֵ�ֱ�Ϊc, d; ��x=-mʱ��P, Q��ֵ�ֱ�Ϊe, f,����c��d, e, f�ĸ��������У������ж���ȷ���� (ֻҪ����ż���).
����������ȵ�����������������Ϊ�෴������������������������������������������������һ����������������һ������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com