
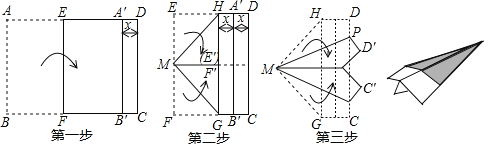
【题目】折纸飞机是我们儿时快乐的回忆,现有一张长为290mm,宽为200mm的白纸,如图所示,以下面几个步骤折出纸飞机:(说明:第一步:白纸沿着EF折叠,AB边的对应边A′B′与边CD平行,将它们的距离记为x;第二步:将EM,MF分别沿着MH,MG折叠,使EM与MF重合,从而获得边HG与A′B′的距离也为x),则PD=______mm.
【答案】![]()
【解析】
延长ME′交CD于T,在TM上截取TW=TP,设DP=m.构建方程可求得x=30,TW=TP可知∠PWT=45°,∠PMW=22.5°,进而∠WMP=∠WPM=22.5°,可求得MW=PW=![]() (100-m)可构建方程
(100-m)可构建方程![]() (100-m)+100-m=16,解得m=(260-160
(100-m)+100-m=16,解得m=(260-160![]() )mm,即可解决问题.
)mm,即可解决问题.
解:延长ME′交CD于T,在TM上截取TW=TP,设DP=m.
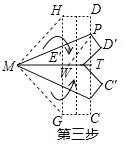
由题意MW=WM=100,MT=160
3x=290-200
x=30
∵TW=TP
∴∠PWT=45°
∵∠PWT=∠PMT+∠MPW,∠PMW=22.5°
∴∠WMP=∠WPM=22.5°
∴MW=PW=![]() (100-m)
(100-m)
∴![]() (100-m)+100-m=160
(100-m)+100-m=160
解得m=(260-160![]() )mm
)mm
∴PD=(260-160![]() )mm
)mm
故答案为260-160![]()


科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有____名;
(2)在扇形统计图中,m的值为____,表示“D等级”的扇形的圆心角为____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形中,如果已知2个元素(其中至少有一个是边),那么就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
(1)观察下列4幅图,根据图中已知元素,可以求出其余未知元素的三角形是 .
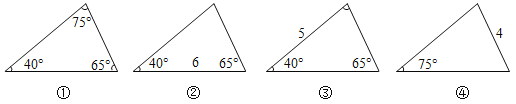
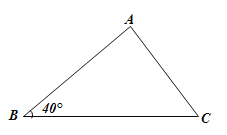
(2)如图,在△ABC中,已知∠B=40°,BC=18,AB=15,请求出AC的长度(答案保留根号).(参考数据:sin40°≈0.6,cos40°≈0.8,tan40°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
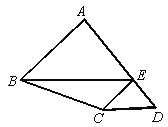
【题目】如图,在四边形ABCD 中,点E在AD上,EC∥AB,EB∥DC,若△ABE面积为5,△ECD的面积为1,则△BCE的面积是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A,B两点(点A在点B左边),与y轴交于点C.
与x轴交于点A,B两点(点A在点B左边),与y轴交于点C.
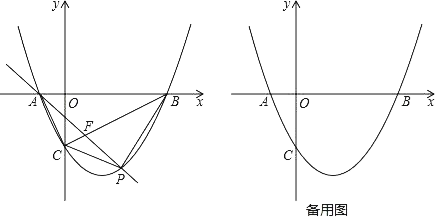
(1)求A,B两点的坐标.
(2)点P是线段BC下方的抛物线上的动点,连结PC,PB.
①是否存在一点P,使△PBC的面积最大,若存在,请求出△PBC的最大面积;若不存在,试说明理由.
②连结AC,AP,AP交BC于点F,当∠CAP=∠ABC时,求直线AP的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有点A、B,且点A表示﹣4,AB=10.
(1)点B表示的有理数为 .
(2)一只小虫从点A出发,以每秒1个单位长度的速度沿数轴正方向爬行到点C,点M、N分别是AC、BC的中点.
①若爬行4秒,则M表示数 ;N表示数 ;MN= .
②若爬行16秒,则M表示数 ;线段MN= .
③若爬行t秒,则线段MM= .
发现:点A、B、C在同一直线上,点M、N分别是AC、BC的中点,已知MN=a,则AB= (用含a的式子表示)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可销售20件每件盈利40元.为了扩大销售,增加盈利,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价5元,商场平均每天可多售出10件,求:
(1)若商场每件衬衫降价10元,则商场每天可盈利多少元?
(2)若商场平均每天要盈利1250元,每件衬衫应降价多少元?
(3)要使商场平均每天盈利1500元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
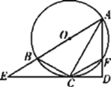
【题目】如图,已知AB为⊙O的直径,C为⊙O上一点,CE与⊙O切于点C,交AB的延长线于点E,过点A作AD⊥EC交EC的延长线于点D,交⊙O于点F,连接BC,CF.
(1)求证:AC平分∠BAD;
(2)若AD=6,∠BAF=60°,求四边形ABCF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com