
【题目】如图,一块四边形草地ABCD,其中∠B=90°,AB=4m,BC=3m,AD=12m,CD=13cm,求这块草地的面积.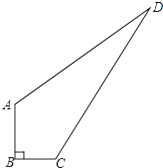
【答案】解:连结AC, 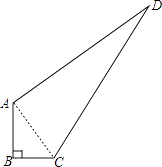
在△ABC中,
∵∠B=90°,AB=4m,BC=3m,
∴AC= ![]() =5(m),
=5(m),
S△ABC= ![]() ×3×4=6(m2),
×3×4=6(m2),
在△ACD中,
∵AD=12m,AC=5m,CD=13m,
∴AD2+AC2=CD2,
∴△ACD是直角三角形,
∴S△ACD= ![]() ×5×12=30(m2).
×5×12=30(m2).
∴四边形ABCD的面积=S△ABC+S△ACD=6+30=36(m2).
【解析】抓住已知条件∠B=90°,因此连接AC,构造直角三角形,将要所求的问题转化到直角三角形中求解。利用勾股定理及逆定理即可求得这块草地的面积。
【考点精析】关于本题考查的勾股定理的概念和勾股定理的逆定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能得出正确答案.


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图①,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系;
(2)①将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
②若AB=2![]() ,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系, ![]() 为坐标原点,点
为坐标原点,点![]() ,点
,点![]() .
.
(1)求![]() 的度数;
的度数;
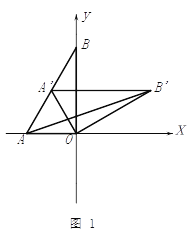
(2)如图1,将⊿![]() 绕点
绕点![]() 顺时针得⊿
顺时针得⊿![]() ,当
,当![]() 恰好落在
恰好落在![]() 边上时,设⊿
边上时,设⊿![]() 的面积为
的面积为![]() ,⊿
,⊿![]() 的面积为
的面积为![]() ,
,![]() 与
与![]() 有何关系?为什么?
有何关系?为什么?
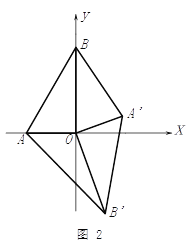
(3)若将⊿![]() 绕点
绕点![]() 顺时针旋转到如图2所示的位置,
顺时针旋转到如图2所示的位置, ![]() 与
与![]() 的关系发生变化了吗?证明你的判断.
的关系发生变化了吗?证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com