
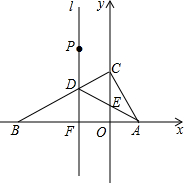
 如图,平面直角坐标系中,$A(\sqrt{3},0),B({-3\sqrt{3},0}),C(0,3)$,l是AB的垂直平分线交BC于D,交x轴于F,连接AD交y轴于E,P为l上D点上一点,且DP=DE,将△DCE绕E逆时针旋转后,边CE交线段DC于M,边DE交线段DF于N,连接PM,若PM=3DN,则点N的坐标为(-$\sqrt{3}$,$\frac{17-\sqrt{33}}{8}$).
如图,平面直角坐标系中,$A(\sqrt{3},0),B({-3\sqrt{3},0}),C(0,3)$,l是AB的垂直平分线交BC于D,交x轴于F,连接AD交y轴于E,P为l上D点上一点,且DP=DE,将△DCE绕E逆时针旋转后,边CE交线段DC于M,边DE交线段DF于N,连接PM,若PM=3DN,则点N的坐标为(-$\sqrt{3}$,$\frac{17-\sqrt{33}}{8}$). 分析 先证明△DCE、△PDC是边长为2的等边三角形,再证明△DEN≌△CEM,得DN=CM,设DN=CM=a,则PM=3a,在RT△PMG中利用勾股定理列出方程即可解决问题.
解答 解:如图所示,连接PC,作MG⊥PC于G.
∵$A(\sqrt{3},0),B({-3\sqrt{3},0}),C(0,3)$,
∴tan∠CBO=$\frac{CO}{BO}$=$\sqrt{3}$,tan∠CAO=$\frac{CO}{AO}$=$\sqrt{3}$,
∴∠CBO=30°,∠CAO=60°,∠ACB=90°,
∴BC=2CO=6,
∵DF垂直平分AB,
∴BD=DA,∠DBA=∠DAB=30°,
∴BD=DA=4,DF═DP=2,DC=2,∠CDA=∠DAB+∠DAB=60°,
∴△CDE是等边三角形,
∵DP=DC,∠PDC=60°,
∴△CDP是等边三角形,
∵∠MEN=∠DEC=60°,
∴∠DEN=∠MEC,
在△DEN和△CEM中,
$\left\{\begin{array}{l}{∠MCE=∠EDN=60°}\\{DE=DC}\\{∠DEN=∠CEM}\end{array}\right.$,
∴△DEN≌△CEM,
∴DN=CM,设DN=a,则CM=a,PM=3a,
在RT△CMG中,∵∠MGC=90°,∠MCG=60°,CM=a,
∴CG=$\frac{a}{2}$,GM=$\frac{\sqrt{3}a}{2}$,PG=2-$\frac{\sqrt{3}a}{2}$,
在RT△PGM中,∵PM2=PG2+MG2,
∴(3a)2=(2-$\frac{a}{2}$)2+($\frac{\sqrt{3}a}{2}$)2,
∴a=$\frac{-1+\sqrt{33}}{8}$或$\frac{-1-\sqrt{33}}{8}$(不合题意舍弃)
∴NF=DF-DN=$\frac{17-\sqrt{33}}{8}$.
∴N(-$\sqrt{3}$,$\frac{17-\sqrt{33}}{8}$),
故答案为N(-$\sqrt{3}$,$\frac{17-\sqrt{33}}{8}$).
点评 本题考查旋转变换、全等三角形的判定和性质、等边三角形的判定和性质、勾股定理等知识,解题的关键是寻找全等三角形,学会利用勾股定理列方程解决问题,属于中考填空题中的压轴题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | 2 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 摸球的次数n | 200 | 500 | 800 | 1000 |
| 摸到白球的概率$\frac{m}{n}$ | 0.62 | 0.604 | 0.601 | 0.599 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com