练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    关于x的一元二次方程（a﹣1）x2+x+a2﹣1=0的一个根是0，则a的值为（）

          A．                       1    B．                       ﹣1 C．                       1或﹣1    D．


    B．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点．此时，竹竿与这一点相距8m，与旗杆相距22m，则旗杆的高为（）

          A．                       12m                            B． 10m                      C．   8m   D． 7m

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若，则=（）

          A．                           B．                           C．                           D．  

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    2x2+5x﹣1=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在平面直角坐标系中，O为原点，直线l：x=1，点A（2，0），点E，点F，点M都在直线l上，且点E和点F关于点M对称，直线EA与直线OF交于点P．

    （Ⅰ）若点M的坐标为（1，﹣1），

    ①当点F的坐标为（1，1）时，如图，求点P的坐标；

    ②当点F为直线l上的动点时，记点P（x，y），求y关于x的函数解析式．

    （Ⅱ）若点M（1，m），点F（1，t），其中t≠0，过点P作PQ⊥l于点Q，当OQ=PQ时，试用含t的式子表示m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    方程x2=9的解为．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    阅读例题：请参照例题的方法解方程x2﹣|x﹣1|﹣1=0

    解方程：x2﹣|x|﹣2=0

    解：（1）当x≥0时，得x2﹣x﹣2=0，

    解得x1=2，x2=﹣1＜0（舍去）．

    （2）当x＜0时，得x2+x﹣2=0，

    解得x1=1 （舍去），x2=﹣2．

    ∴原方程的解为x1=2，x2=﹣2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知关于x的方程x2+mx﹣6=0的一个根为2，则m=．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知抛物线经过A（﹣3，0），B（1，0），C（2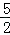，）三点，其对称轴交x轴于点H，一次函数y=kx+b（k≠0）的图象经过点C，与抛物线交于另一点D（点D在点C的左边），与抛物线的对称轴交于点E．

    （1）求抛物线的解析式；

    （2）如图1，当S△EOC=S△EAB时，求一次函数的解析式；

    （3）如图2，设∠CEH=α，∠EAH=β，当α＞β时，直接写出k的取值范围．

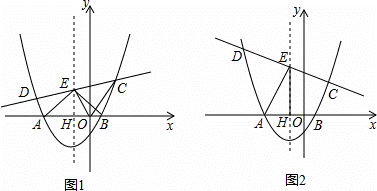
    查看答案和解析>>

    同步练习册答案