
在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,点F,点M都在直线l上,且点E和点F关于点M对称,直线EA与直线OF交于点P.
(Ⅰ)若点M的坐标为(1,﹣1),
①当点F的坐标为(1,1)时,如图,求点P的坐标;
②当点F为直线l上的动点时,记点P(x,y),求y关于x的函数解析式.
(Ⅱ)若点M(1,m),点F(1,t),其中t≠0,过点P作PQ⊥l于点Q,当OQ=PQ时,试用含t的式子表示m.

解:(Ⅰ)①∵点O(0,0),F(1,1),
∴直线OF的解析式为y=x.
设直线EA的解析式为:y=kx+b(k≠0)、
∵点E和点F关 于点M(1,﹣1)对称,
于点M(1,﹣1)对称,
∴E(1,﹣3).
又A(2,0),点E在直线EA上,
∴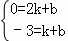 ,
,
解得 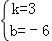 ,
,
∴直线EA的解析式为:y=3x﹣6.
∵点P是直线OF与直线EA的交点,则 ,
,
解得  ,
,
∴点P的坐标是(3,3).
②由已知可设点F的坐标是(1,t).
∴直线OF的解析式为y=tx.
设直线EA的解析式为y=cx+d(c、d是常数,且c≠0).
由点E和点F关于点M(1,﹣1)对称,得点E(1,﹣2﹣t).
又点A、E在直线EA上,
∴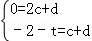 ,
,
解得 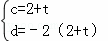 ,
,
∴直线EA的解析式为:y=(2+t)x﹣2(2+t).
∵点P为直线OF与直线EA的交点,
∴tx=( 2+t)x﹣2(2+t),即t=x﹣2.
2+t)x﹣2(2+t),即t=x﹣2.
则有 y=tx=(x﹣2)x=x2﹣2x;
(Ⅱ)由(Ⅰ)可得,直线OF的解析式为y=tx.
直线EA的解析式为y=(t﹣2m)x﹣2(t﹣2m).
∵点P为直线OF与直线EA的交点,
∴tx=(t﹣2m)x﹣2(t﹣2m),
化简,得 x=2﹣ .
.
有 y=tx=2t﹣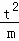 .
.
∴点P的坐标为(2﹣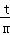 ,2t﹣
,2t﹣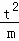 ).
).
∵PQ⊥l于点Q,得点Q(1,2t﹣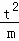 ),
),
∴OQ2=1+t2(2﹣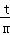 )2,PQ2=(1﹣
)2,PQ2=(1﹣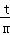 )2,
)2,
∵OQ=PQ,
∴1+t2(2﹣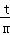 )2=(1﹣
)2=(1﹣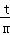 )2,
)2,
化简,得 t(t﹣2m)(t2﹣2mt﹣1)=0.
又∵t≠0,
∴t﹣2m=0或t2﹣2mt﹣1=0,
解得 m=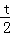 或m=
或m=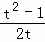 .
.
则m=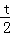 或m=
或m= 即为所求.
即为所求.



科目:初中数学 来源: 题型:
如图,在梯形ABCD中,AD∥BC,AD=3,CD=5,BC=10,梯形的高为4,动点M从点B出发沿线段BC以每秒2个单位长度向终点C运动;动点N同时从点C出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒
(1)直接写出梯形ABCD的中位线长;
(2)当MN∥AB时,求t的值;
(3)试探究:t为何值时,使得MC=MN.

查看答案和解析>>
科目:初中数学 来源: 题型:
我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,如将(101)2,(1011)2换算成十进制数应为:(101)2=1×22+0×21+1×20=4+0+1=5,
(1011)2=1×23+0×22+1×21+1×20=11.
按此方式,将二进制(1001)2换算成十进 制数的结果是.
制数的结果是.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的一元二次方程x2﹣mx﹣2=0.
(1)若﹣1是方程的一个根,求m的值和方程的另一个根.
(2)对于任意实数m,判断方程根的情况,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的一元二次方程x2﹣4x+m=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程 两实数根为x1,x2,且满足5x1+2x2=2,求实数m的值.
两实数根为x1,x2,且满足5x1+2x2=2,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com