
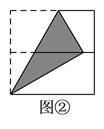
【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).



A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,∠B <∠C,AD,AE分别是△ABC的高和角平分线。
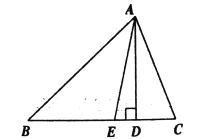
(1)若∠B=30°,∠C=50°,试确定∠DAE的度数;
(2)试写出∠DAE,∠B,∠C的数量关系,并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
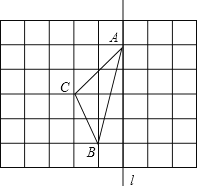
【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与关于直线![]() 成轴对称的△A′B′C′;
成轴对称的△A′B′C′;
(2)线段CC′被直线![]() ;
;
(3)△ABC的面积为 ;
(4)在直线![]() 上找一点P,使PB+PC的长最短.
上找一点P,使PB+PC的长最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
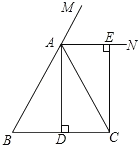
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
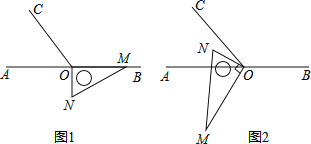
(1)将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的过程中,假如第t秒时,OA、OC、ON三条射线构成相等的角,求此时t的值为多少?
(2)将图1中的三角板绕点O顺时针旋转图2,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
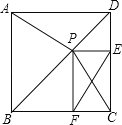
【题目】如图,P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足.
(1)求证:△APD≌△CPD;
(2)若CF=3,CE=4,求AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com