
【题目】若x2+kx+25是一个完全平方式,则k=_______.
科目:初中数学 来源: 题型:
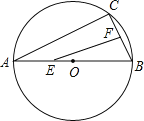
【题目】如图,AB是⊙O的直径,弦BC=4cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B方向运动,设运动时间为t(秒),连结EF,当t值为 秒时,△BEF是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
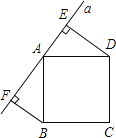
【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是以定长AB为直径的⊙O,CD为![]() 上的一条动弦(点C与A,点D与B不重合),CF⊥CD交AB于F,DE⊥CD交AB于E.
上的一条动弦(点C与A,点D与B不重合),CF⊥CD交AB于F,DE⊥CD交AB于E.
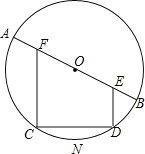
(1)求证:AF=BE;
(2)若弦CD的长度保持不变,四边形CDEF的面积是否也保持不变?并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
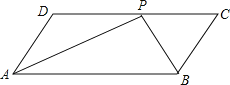
(1)求∠APB的度数;
(2)如果AD=5cm,AP=8cm,求△APB的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
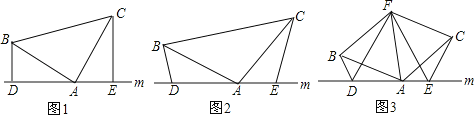
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.猜测DE、BD、CE三条线段之间的数量关系(直接写出结果即可).
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问第(1)题中DE、BD、CE之间的关系是否仍然成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断线段DF、EF的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com