
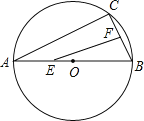
【题目】如图,AB是⊙O的直径,弦BC=4cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B方向运动,设运动时间为t(秒),连结EF,当t值为 秒时,△BEF是直角三角形.
【答案】2或3.5.
【解析】
试题分析:由AB是⊙O的直径,弦BC=4cm,F是弦BC的中点,∠ABC=60°.可求得AB的长,又由△BEF是直角三角形,可得当∠BEF=90°与∠BFE=90°,继而求得答案.
解:∵AB是⊙O的直径,
∴∠C=90°,
∵弦BC=4cm,F是弦BC的中点,
∴BF=2cm,
∵∠ABC=60°,
∴AB=2BC=8(cm),
∴若∠BFE=90°,则BE=2BF=4cm,
∴AE=AB﹣BE=4cm,
即t=4÷2=2(s);
若∠BEF=90°,
则BE=![]() BF=1(cm),
BF=1(cm),
∴AE=AB﹣BE=7(cm),
∴t=7÷2=3.5(s),
∴t值为2或3.5秒时,△BEF是直角三角形.
故答案为:2或3.5.


科目:初中数学 来源: 题型:
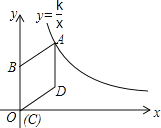
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=![]() (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=![]() (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列描述不属于定义的是( )
A.两组对边分别平行的四边形叫做平行四边形;
B.正三角形是特殊的等腰三角形;
C.在同一平面内三条线段首尾顺次连接得到的图形叫做三角形;
D.含有未知数的等式叫做方程
查看答案和解析>>
科目:初中数学 来源: 题型:
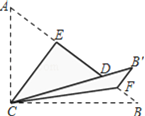
【题目】如图, 在Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相垂直平分且相等的四边形是正方形
D.一组对边相等,另一组对边平行的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“420”雅安地震后,某商家为支援灾区人民,计划捐赠帐篷16800顶,该商家备有2辆大货车、8辆小货车运送帐篷.计划大货车比小货车每辆每次多运帐篷200顶,大、小货车每天均运送一次,两天恰好运完.
(1)求大、小货车原计划每辆每次各运送帐篷多少顶?
(2)因地震导致路基受损,实际运送过程中,每辆大货车每次比原计划少运200m顶,每辆小货车每次比原计划少运300顶,为了尽快将帐篷运送到灾区,大货车每天比原计划多跑![]() 次,小货车每天比原计划多跑m次,一天恰好运送了帐篷14400顶,求m的值.
次,小货车每天比原计划多跑m次,一天恰好运送了帐篷14400顶,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.
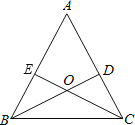
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com