
【题目】已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.
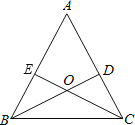
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由.
【答案】(1)证明见解析(2)点O在∠BAC的角平分线上,理由见解析
【解析】
试题分析:(1)由OB=OC,即可求得∠OBC=∠OCB,又由,锐角△ABC的两条高BD、CE相交于点O,根据三角形的内角和等于180°,即可证得△ABC是等腰三角形;
(2)首先连接AO并延长交BC于F,通过证△AOB≌△AOC(SSS),得到∠BAF=∠CAF,即点O在∠BAC的角平分线上.
(1)证明:∵OB=OC,
∴∠OBC=∠OCB,
∵锐角△ABC的两条高BD、CE相交于点O,
∴∠BEC=∠CDB=90°,
∵∠BEC+∠BCE+∠ABC=∠CDB+∠DBC+∠ACB=180°,
∴180°﹣∠BEC﹣∠BCE=180°﹣∠CDB﹣∠CBD,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形;
(2)解:点O在∠BAC的角平分线上.
理由:连接AO并延长交BC于F,
在△AOB和△AOC中,
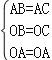
∴△AOB≌△AOC(SSS).
∴∠BAF=∠CAF,
∴点O在∠BAC的角平分线上.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论:(1)BP=CM;(2)△ABQ≌△CAP;(3)∠CMQ的度数始终等于60°;(4)当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形.其中正确的结论有( )
秒时,△PBQ为直角三角形.其中正确的结论有( )
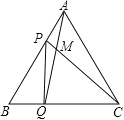
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦BC=4cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B方向运动,设运动时间为t(秒),连结EF,当t值为 秒时,△BEF是直角三角形.
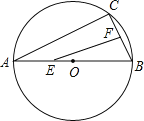
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中装有两个相同的小球,它们的标号分别为2和5,乙口袋中装有两个相同的小球,它们的标号分别为4和9,丙口袋中装有三个相同的小球,它们的标号分别为1,6,7.从这3个口袋中各随机取出一个小球.
(1)用树形图表示所有可能出现的结果;
(2)若用取出的三个小球的标号分别表示三条线段的长,求这些线段能构成三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为 .
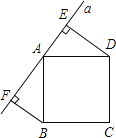
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是以定长AB为直径的⊙O,CD为![]() 上的一条动弦(点C与A,点D与B不重合),CF⊥CD交AB于F,DE⊥CD交AB于E.
上的一条动弦(点C与A,点D与B不重合),CF⊥CD交AB于F,DE⊥CD交AB于E.
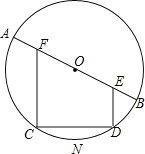
(1)求证:AF=BE;
(2)若弦CD的长度保持不变,四边形CDEF的面积是否也保持不变?并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
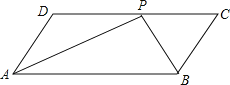
(1)求∠APB的度数;
(2)如果AD=5cm,AP=8cm,求△APB的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P的横坐标是-3,且点P到x轴的距离为5,则P的坐标是( )
A. (-3,5)或(-3,-5) B. (5,-3)或(-5,-3)
C. (-3,5) D. (-3,-3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com