
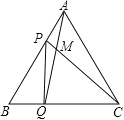
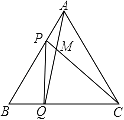
【题目】如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论:(1)BP=CM;(2)△ABQ≌△CAP;(3)∠CMQ的度数始终等于60°;(4)当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形.其中正确的结论有( )
秒时,△PBQ为直角三角形.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】试题分析:易证△ABQ≌△CAP,可得∠AQB=∠CPA,即可求得∠AMP=∠B=60°,易证∠CQM≠60°,可得CQ≠CM,根据t的值易求BP,BQ的长,即可求得PQ的长,即可解题. ∵△ABC是等边三角形,
∴AB=BC=AC,∠BAC=∠B=∠ACB=60°, 根据题意得:AP=BQ, 在△ABQ和△CAP中,
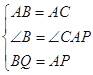 , ∴△ABQ≌△CAP(SAS),(2)正确; ∴∠AQB=∠CPA,
, ∴△ABQ≌△CAP(SAS),(2)正确; ∴∠AQB=∠CPA,
∵∠BAQ+∠APC+∠AMP=180°,∠BAQ+∠B+∠AQB=180°, ∴∠AMP=∠B=60°,
∴∠QMC=60°,(3)正确; ∵∠QMC=60°,∠QCM≠60°, ∴∠CQM≠60°, ∴CQ≠CM,
∵BP=CQ, ∴CM≠BP,(1)错误; 当t=![]() 时,BQ=
时,BQ=![]() ,BP=4﹣
,BP=4﹣![]() =
=![]() ,
,
∵PQ2=BP2+BQ2﹣2BPBQcos60°, ∴PQ=![]() , ∴△PBQ为直角三角形,
, ∴△PBQ为直角三角形,
同理t=![]() 时,△PBQ为直角三角形仍然成立,(4)正确;
时,△PBQ为直角三角形仍然成立,(4)正确;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
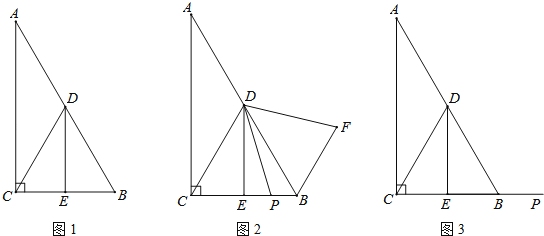
(1)如图1,DE与BC的数量关系是 ;
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n是方程x2﹣2x﹣1=0的两根,且(7m2﹣14m+a)(3n2﹣6n﹣7)=8,则a的值等于( ).
A.﹣5 B.5 C.﹣9 D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列描述不属于定义的是( )
A.两组对边分别平行的四边形叫做平行四边形;
B.正三角形是特殊的等腰三角形;
C.在同一平面内三条线段首尾顺次连接得到的图形叫做三角形;
D.含有未知数的等式叫做方程
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在外来文化的渗透和商家的炒作下,过洋节俨然成为现今青少年一种时尚,圣诞节前期,三位同学到某超市调研一种进价为每个2元的苹果的销售情况,请根据小丽提供的信息,解答小华和小明提出的问题.
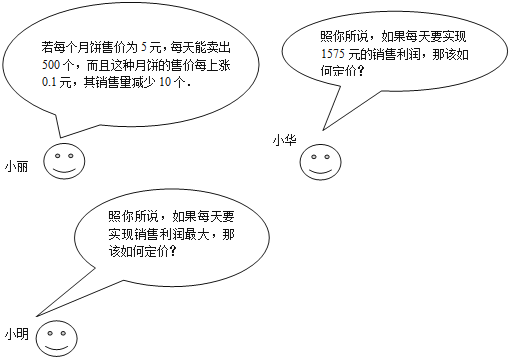
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为__________
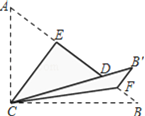
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相垂直平分且相等的四边形是正方形
D.一组对边相等,另一组对边平行的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.
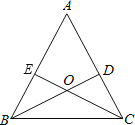
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com