
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
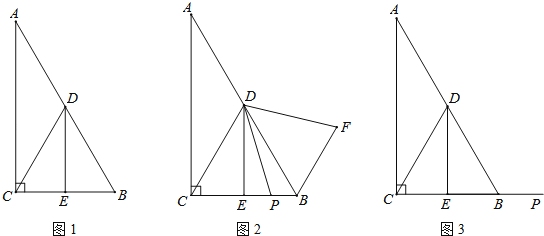
(1)如图1,DE与BC的数量关系是 ;
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.
【答案】(1)DE=![]() BC(2)BF+BP=
BC(2)BF+BP=![]() DE.理由见解析(3)
DE.理由见解析(3)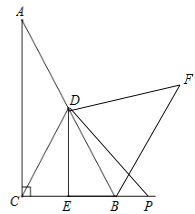 ,BF﹣BP=
,BF﹣BP=![]() DE
DE
【解析】
试题分析:(1)由∠ACB=90°,∠A=30°得到∠B=60°,根据直角三角形斜边上中线性质得到DB=DC,则可判断△DCB为等边三角形,由于DE⊥BC,DE=![]() BC;
BC;
(2)根据旋转的性质得到∠PDF=60°,DP=DF,易得∠CDP=∠BDF,则可根据“SAS”可判断△DCP≌△DBF,则CP=BF,利用CP=BC﹣BP,DE=![]() BC可得到BF+BP=
BC可得到BF+BP=![]() DE;
DE;
(3)与(2)的证明方法一样得到△DCP≌△DBF得到CP=BF,而CP=BC+BP,则BF﹣BP=BC,所以BF﹣BP=![]() DE.
DE.
解:(1)∵∠ACB=90°,∠A=30°,
∴∠B=60°,
∵点D是AB的中点,
∴DB=DC,
∴△DCB为等边三角形,
∵DE⊥BC,
∴DE=![]() BC;
BC;
故答案为DE=![]() BC.
BC.
(2)BF+BP=![]() DE.理由如下:
DE.理由如下:
∵线段DP绕点D逆时针旋转60°,得到线段DF,
∴∠PDF=60°,DP=DF,
而∠CDB=60°,
∴∠CDB﹣∠PDB=∠PDF﹣∠PDB,
∴∠CDP=∠BDF,
在△DCP和△DBF中
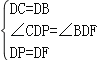 ,
,
∴△DCP≌△DBF(SAS),
∴CP=BF,
而CP=BC﹣BP,
∴BF+BP=BC,
∵DE=![]() BC,
BC,
∴BC=![]() DE,
DE,
∴BF+BP=![]() DE;
DE;
(3)如图,
与(2)一样可证明△DCP≌△DBF,
∴CP=BF,
而CP=BC+BP,
∴BF﹣BP=BC,
∴BF﹣BP=![]() DE.
DE.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
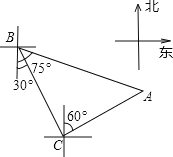
【题目】轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.
A.25![]() B.25
B.25![]() C.50 D.25
C.50 D.25
查看答案和解析>>
科目:初中数学 来源: 题型:
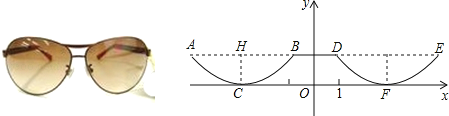
【题目】如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm.则右轮廓线DFE所在抛物线的函数解析式为( )
A.y=![]() (x+3)2
(x+3)2
B.y=![]() (x+3)2
(x+3)2
C.y=![]() (x﹣3)2
(x﹣3)2
D.y=![]() (x﹣3)2
(x﹣3)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x﹣20)°,则∠α的度数为( )
A. 70° B. 86° C. 70°或86° D. 30°或38°
查看答案和解析>>
科目:初中数学 来源: 题型:
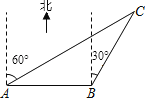
【题目】在一自助夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),那么,由此可知,B、C两地相距 m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年济宁市常住人口约为820万人,与2010年第六次人口普查的808.19万人略有提升,820万用科学记数法表示为8.2×10n,则n= .
查看答案和解析>>
科目:初中数学 来源: 题型:
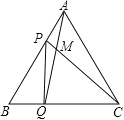
【题目】如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论:(1)BP=CM;(2)△ABQ≌△CAP;(3)∠CMQ的度数始终等于60°;(4)当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形.其中正确的结论有( )
秒时,△PBQ为直角三角形.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com