Question

6．已知∠AOB，求作∠A′O′B′，使∠A′O′B′=∠AOB，并证明．
作法：①以O为圆心，任意长为半径画弧分别交OA、OB于点M、N
②画一条射线O′A′，以O′为圆心，OM长为半径画弧交O′A′于点M′
③以点M′为圆心，MN长为半径画弧与第②步中所画弧交于点N′
④过点N′画射线O′B′，则∠A′O′B′=∠AOB
证明：

Answer 1

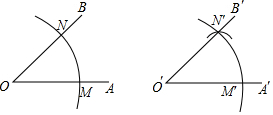
分析 根据作一个角等于已知角的步骤作出∠A′O′B′=∠AOB，再由SSS定理得出△OMN≌△O′M′N′，根据全等三角形的性质即可得出结论．

解答 解：作法：①以O为圆心，任意长为半径画弧分别交OA、OB于点M、N
②画一条射线O′A′，以O′为圆心，OM长为半径画弧交O′A′于点M′
③以点M′为圆心，MN长为半径画弧与第②步中所画弧交于点N′
④过点N′画射线O′B′，则∠A′O′B′=∠AOB．
故答案为：任意，OM，MN．
证明：在△OMN与△O′M′N′，
∵$\left\{\begin{array}{l}{OM=O′M}\\{ON=O′N′}\\{MN=MN′}\end{array}\right.$，
∴△OMN≌△O′M′N′（SSS），
∴∠A′O′B′=∠AOB．

点评 本题考查的是作图-基本作图，熟知作一个角等于已知角的步骤及全等三角形的判定与性质是解答此题的关键．