
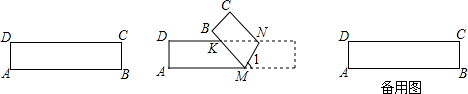
分析 (1)根据矩形的性质和折叠的性质求出∠KNM,∠KMN的度数,根据三角形内角和即可求解;
(2)当折痕MN与对角线AC重合时,此时△AKC为等腰三角形,设MK=AK=CK=x,则DK=5-x,在Rt△ADK中,根据勾股定理得:AD2+DK2=AK2,
即12+(5-x)2=x2,求得x=2.6,所以MK=AK=CK=2.6,根据三角形面积公式即可解答;
(3)不能,过M点作ME⊥DN,垂足为E,通过证明NK>1,由三角形面积公式可得△MNK的面积不可能小于0.5.
解答 解:(1)∵四边形ABCD是矩形,
∴AM∥DN,
∴∠KNM=∠1,
∵∠KMN=∠1,
∴∠KNM=∠KMN,
∵∠1=70°,
∴∠KNM=∠KMN=70°,
∴∠MKN=40°;
(2)如图1,
折痕即为AC,此时△AKC为等腰三角形,
设MK=AK=CK=x,则DK=5-x,
在Rt△ADK中,根据勾股定理得:AD2+DK2=AK2,
即12+(5-x)2=x2,
解得:x=2.6,
∴MK=AK=CK=2.6,
${S}_{△MNK}={S}_{△ACK}=\frac{1}{2}×1×2.6=1.3$
∴△MNK的面积的为1.3.
(3)不能,如图2,
理由如下:过M点作AE⊥DN,垂足为点E,则ME=AD=1,
由(1)知,∠KNM=∠KMN,
∴MK=NK,
又∵MK≥ME,ME=AD=1,
∴MK≥1,
又∵${S}_{△MNK}=\frac{1}{2}NK•ME≥\frac{1}{2}$,
即△MNK面积的最小值为$\frac{1}{2}$,不可能小于0.5.
点评 本题主要考查了翻折变换的性质、勾股定理,解决本题的关键是利用翻折变换的性质得到相等的角,掌握辅助线的作法,注意掌握数形结合思想.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,D,E是BC的三等分点,BC=15cm,AD=13cm,AE=12cm,F,G分别是AB,AC的中点,求四边形DEGF的周长和面积.
如图,在△ABC中,D,E是BC的三等分点,BC=15cm,AD=13cm,AE=12cm,F,G分别是AB,AC的中点,求四边形DEGF的周长和面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
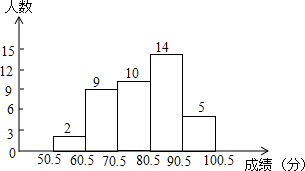 初三某班对最近一次数学测验成绩(得分取整数) 进行统计分析,将所有成绩由低到高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的 信息,回答下列问题:
初三某班对最近一次数学测验成绩(得分取整数) 进行统计分析,将所有成绩由低到高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的 信息,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
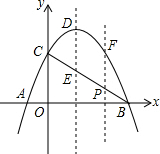 已知抛物线y=-x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且顶点为D(1,4).
已知抛物线y=-x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且顶点为D(1,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com