
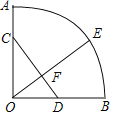
【题目】如图线段OA=12,线段OA绕点O旋转90°,形成扇形OAB,点D为OB的中点,点E为弧AB上的动点,连接OE,与CD的交点为F,点C在OA上,AC=4.
(1)①CD= ;②当BE弧长为4π时,∠BOE= .
(2)当四边形ODEC面积最大时,求EF.
(3)在点E的运动过程中,是否存在一个时刻使CE+2DE有最小值?若存在请直接写出答案;若不存在,请说明理由.
【答案】(1)①10;②60°;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)运用勾股定理计算CD,由弧长公式可求出∠BOE;
(2)四边形面积最大时,两三角形的高的和等于半径,即可求得EF;
(3)延长OB至点G,使BG=OB,连接GE、GC、DE.证明△DOE~△EOG,得到EG=2DE,所以CE+2DE=CE+EG,当C、E、G三点在同一直线上上时,CE+EG最小,此时CE+EG=CG=![]() =
=![]() =8
=8![]() ,即CE+2DE有最小值为8
,即CE+2DE有最小值为8![]() .
.
解:(1)①在Rt△OCD中,∠COD=90°,OC=OA﹣AC=12﹣4=8,OD=![]() OB=
OB=![]() =6,
=6,
∴![]() =
=![]() =10,
=10,
故答案为:10;
②设∠BOE=n°,由弧长公式得:![]() ,解得:n=6
,解得:n=6
∴∠BOE=60°;
故答案为:60°;
(2)分别过O、E作OM⊥CD于M,EN⊥CD于N,
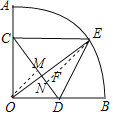
∵CD=10,
∴S四边形ODEC=S△OCD+S△CDE=![]() CD(OM+EN)≤
CD(OM+EN)≤![]() CDOE=
CDOE=![]() ×10×12=60;
×10×12=60;
此时,OM、EN、OE重合,
∵OMCD=OCOD
∴10×OM=6×8,OM=![]() ,
,
∴![]() =
=![]() ;
;
(3)延长OB至点G,使BG=OB,连接GE、GC、DE.

∴![]()
∵点D为OB的中点,OB=OE,
∴![]() ,
,
∴![]() ,
,
又∠DOE=∠EOG,
∴△DOE~△EOG,
![]() ,
,
即EG=2DE,
∴CE+2DE=CE+EG,
当C、E、G三点在同一直线上上时,CE+EG最小,
CO=OA﹣AC=12﹣4=8,OG=OB+BG=12+12=24,
此时CE+EG=CG=![]() =
=![]() =8
=8![]() ,
,
故CE+2DE有最小值为8![]() .
.


科目:初中数学 来源: 题型:
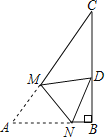
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AB=3,点M,N分别在线段AC,AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,若△DCM为直角三角形时,则AM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在精准扶贫中,李师傅在扶贫工作者的指导下,计划用8个大棚种植香瓜和甜瓜根据种植经验及市场情况,他打算两个品种同时种,一个大只种一个品种的瓜并预测明年两种瓜的产量、销售价格及成本如下:
品种项目 | 产量(斤/每棚) | 销售价(元/每斤) | 成本(元/棚) |
香瓜 | 2000 | 12 | 8000 |
甜瓜 | 4500 | 3 | 5000 |
根据以上信息,求李师傅至少种植多少个大棚的香瓜,才能使他获得的利润不低于10万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店A类笔的标价是B类笔标价的1.2倍,某顾客用240元买笔,能单独购买A笔的数量恰好比单独购买B类笔的数量少4支.
(1)求A,B两类笔的标价;
(2)若A类笔的进价为8元/支,B类笔的进价为7元/支.文具店老板准备用不超过760元购进两类笔共100支,应如何进货才能获得最大利润?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是等边△ABC内一点,将△DBC绕点B旋转到△EBA的位置,则∠EBD的度数是( )

A. 45°B. 60°C. 90°D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2011年高中招生考试,某中学对全校九年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行,绘制成了如下两幅不完整的统计图,请根据图中所给信息,下列问题:
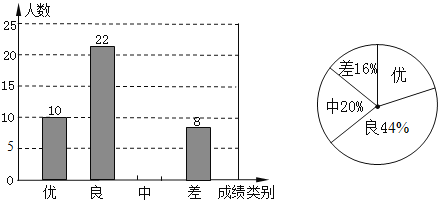
(1)请将表示成绩类别为“中”的条形统计图补充完整;
(2)在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角是 72 度;
(3)学校九年级共有1000人参加了这次数学考试,估算该校九年级共有多少名学生的数学成绩可以达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市九年级学生升学考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(![]() :40分;
:40分;![]() :39-35分;
:39-35分;![]() :34-30分;
:34-30分;![]() :29-20分;
:29-20分;![]() :19-0分) 统计如右表。根据上面提供的信息,回答下列问题:
:19-0分) 统计如右表。根据上面提供的信息,回答下列问题:
(1)在统计表中,![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数”.请问:甲同学的体育成绩应在 分数段内(填相应分数段的字母).
(3)若把成绩在![]() 分以上(含
分以上(含![]() 分)定为优秀,则我市今年8000名九年级学生中体育成绩为优秀的学生人数约有 .名.
分)定为优秀,则我市今年8000名九年级学生中体育成绩为优秀的学生人数约有 .名.
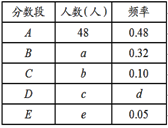
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE是□ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E、连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF:BE=2:3;④S四边形AFOE:S△COD=2:3.其中正确的结论有( )个.
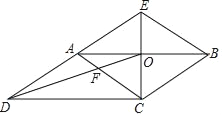
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com