
【题目】如图,点D是等边△ABC内一点,将△DBC绕点B旋转到△EBA的位置,则∠EBD的度数是( )

A. 45°B. 60°C. 90°D. 120°
科目:初中数学 来源: 题型:
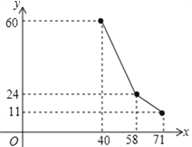
【题目】国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款36000元用来代理品牌服装的销售.已知该品牌服装进价每件40元,日销售y(件)与销售价x(元/件)之间的关系如图所示(实线),每天付员工的工资每人每天82元,每天应支付其它费用106元.
(1)求日销售y(件)与销售价x (元/件)之间的函数关系式;
(2)若暂不考虑还贷,当某天的销售价为48元/件时,收支恰好平衡(收入=支出),求该店员工人数;
(3)若该店只有2名员工,则该店至少需要多少天才能还清贷款,此时,每件服装的价格应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
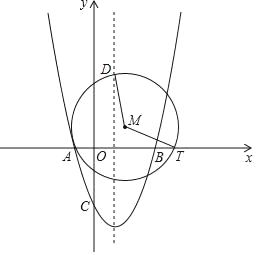
【题目】如图,二次函数y=x2+bx﹣3的图象与x轴分别相交于A、B两点,点B的坐标为(3,0),与y轴的交点为C,动点T在射线AB上运动,在抛物线的对称轴l上有一定点D,其纵坐标为2![]() ,l与x轴的交点为E,经过A、T、D三点作⊙M.
,l与x轴的交点为E,经过A、T、D三点作⊙M.
(1)求二次函数的表达式;
(2)在点T的运动过程中,
①∠DMT的度数是否为定值?若是,请求出该定值:若不是,请说明理由;
②若MT=![]() AD,求点M的坐标;
AD,求点M的坐标;
(3)当动点T在射线EB上运动时,过点M作MH⊥x轴于点H,设HT=a,当OH≤x≤OT时,求y的最大值与最小值(用含a的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=mx2+(2m+4)x+8(m为常数,且m≠0),
(1)证明:该函数与x轴一定有交点;
(2)若该函数经过点A(﹣1+![]() ,y1)B(﹣1,y2),请比较y1,y2的大小关系,并说明理由.
,y1)B(﹣1,y2),请比较y1,y2的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
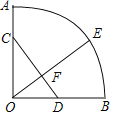
【题目】如图线段OA=12,线段OA绕点O旋转90°,形成扇形OAB,点D为OB的中点,点E为弧AB上的动点,连接OE,与CD的交点为F,点C在OA上,AC=4.
(1)①CD= ;②当BE弧长为4π时,∠BOE= .
(2)当四边形ODEC面积最大时,求EF.
(3)在点E的运动过程中,是否存在一个时刻使CE+2DE有最小值?若存在请直接写出答案;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩n(分) | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n<90 | B | |
70≤n<80 | C | 15 |
n<70 | D | 6 |
根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,抛物线![]() 经过原点,且与x轴相交于点A,点A的横坐标为6,抛物线顶点为点B.
经过原点,且与x轴相交于点A,点A的横坐标为6,抛物线顶点为点B.
(1)求这条抛物线的表达式和顶点B的坐标;
(2)过点O作OP∥AB,在直线OP上点取一点Q,使得∠QAB=∠OBA,求点Q的坐标;
(3)将该抛物线向左平移m(m>0)个单位,所得新抛物线与y轴负半轴相交于点C且顶点仍然在第四象限,此时点A移动到点D的位置,CB:DB=3:4,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com