
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
【答案】(1) 实际每年绿化面积为54万平方米;(2) 则至少每年平均增加72万平方米.
【解析】试题分析:(1)设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.6x万平方米.根据“实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务”列出方程;(2)设平均每年绿化面积增加a万平方米.则由“完成新增绿化面积不超过2年”列出不等式.
试题解析:
(1)设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.6x万平方米,根据题意,得
![]()
解得:x=33.75,
经检验x=33.75是原分式方程的解,
则1.6x=1.6×33.75=54(万平方米).
答:实际每年绿化面积为54万平方米;
(2)设平均每年绿化面积增加a万平方米,根据题意得
54×2+2(54+a)≥360
解得:a≥72.
答:则至少每年平均增加72万平方米.


 能力评价系列答案
能力评价系列答案科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
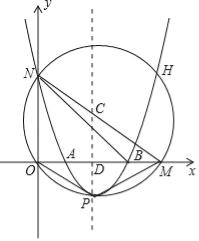
【题目】如图所示,在平面直角坐标系中,⊙C经过坐标原点O,且与x轴,y轴分别相交于M(4,0),N(0,3)两点.已知抛物线开口向上,与⊙C交于N,H,P三点,P为抛物线的顶点,抛物线的对称轴经过点C且垂直x轴于点D.
(1)求线段CD的长及顶点P的坐标;
(2)求抛物线的函数表达式;
(3)设抛物线交x轴于A,B两点,在抛物线上是否存在点Q,使得S四边形OPMN=8S△QAB,且△QAB∽△OBN成立?若存在,请求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x,y为有理数,现规定一种新运算“〇”满足x〇y=y2﹣2x
(1)求5〇(﹣3);
(2)求(5〇x)﹣2(y〇x),其中|x﹣1|+(y+2)4=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:当温度达到设定温度![]() 时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到
时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到![]() 时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至
时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至![]() 时,制冷再次停止,……,按照以上方式循环进行.
时,制冷再次停止,……,按照以上方式循环进行.
同学们记录了44![]() 内15个时间点冷柜中的温度
内15个时间点冷柜中的温度![]() 随时间
随时间![]() 的变化情况,制成下表:
的变化情况,制成下表:
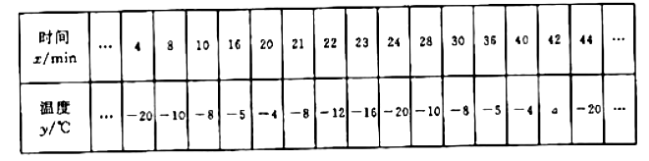
(1)通过分析发现,冷柜中的温度![]() 是时间
是时间![]() 的函数.
的函数.
①当![]() 时,写出一个符合表中数据的函数解析式 ;
时,写出一个符合表中数据的函数解析式 ;
②当![]() 时,写出一个符合表中数据的函数解析式 ;
时,写出一个符合表中数据的函数解析式 ;
(2)![]() 的值为 ;
的值为 ;
(3)如图,在直角坐标系中,已描出了上表中部分数据对应的点,请描出剩余对应的点,并画出![]() 时温度
时温度![]() 随时间
随时间![]() 变化的函数图象.
变化的函数图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数![]() (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com