
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
【答案】(1)y=-![]() (0≤x≤3);(2)抛物线水柱的最大高度为
(0≤x≤3);(2)抛物线水柱的最大高度为![]() m.
m.
【解析】
试题分析:(1)以水管和地面交点为原点,原点与水柱落地点所在直线为x轴适当的直角坐标系,利用顶点式y=a(x-1)2+k,求解析式
(2)利用顶点式y=-![]() (x-1)2+
(x-1)2+![]() (0≤x≤3),知顶点坐标(1,
(0≤x≤3),知顶点坐标(1,![]() ),从而求出水柱的最大高度是
),从而求出水柱的最大高度是![]() 米。
米。
试题解析:(1)如图,以水管与地面交点为原点,原点与水柱落地点所在直线为x轴,水管所在直线为y轴,建立平面直角坐标系.
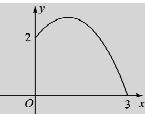
由题意可设抛物线的函数解析式为y=a(x-1)2+h(0≤x≤3)
抛物线过点(0,2)和(3,0),代入抛物线解析式得:
![]()
解得: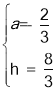
所以,抛物线的解析式为:y=-![]() (x-1)2+
(x-1)2+![]() (0≤x≤3),
(0≤x≤3),
化为一般形式为:y=-![]() (0≤x≤3)
(0≤x≤3)
(2)由(1)知抛物线的解析式为y=-![]() (x-1)2+
(x-1)2+![]() (0≤x≤3),
(0≤x≤3),
当x=1时,y=![]() ,
,
所以,抛物线水柱的最大高度为![]() m.
m.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】(本小题满分14分)
如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(-4,0)、B(0,3),抛物线y=-x2+2x+1与y轴交于点C.
(1)求直线y=kx+b的解析式;
(2)若点P(x,y)是抛物线y=-x2+2x+1上的任意一点,设点P到直线AB的距离为d,求d关于x的函数解析式,并求d取最小值时点P的坐标;
(3)若点E在抛物线y=-x2+2x+1的对称轴上移动,点F在直线AB上移动,求CE+EF的最小值. 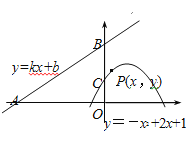
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有21名同学们参加某比赛,预赛成绩各不同,要取前11名参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这21名同学成绩的( )
A.最高分
B.中位数
C.极差
D.平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为( ) 
A.10
B.12
C.16
D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( ) 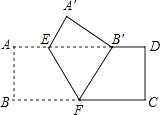
A.12
B.24
C.12 ![]()
D.16 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com