练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知x，y为有理数，现规定一种新运算“〇”满足x〇y＝y2﹣2x

    （1）求5〇（﹣3）；

    （2）求（5〇x）﹣2（y〇x），其中|x﹣1|+（y+2）4＝0

    【答案】（1）﹣1；（2）﹣19．

    【解析】

    （1）根据新定义规定的运算法则计算可得；

    （2）利用新定义规定的运算化简原式，再由非负数的性质得出x和y的值，代入计算可得．

    解：（1）5〇（﹣3）＝（﹣3）2﹣2×5

    ＝9﹣10

    ＝﹣1；

    （2）原式＝x2﹣2×5﹣2（x2﹣2y）

    ＝x2﹣10﹣2x2+4y

    ＝﹣x2+4y﹣10，

    ∵|x﹣1|+（y+2）4＝0，

    ∴x＝1，y＝﹣2，

    则原式＝﹣1﹣8﹣10＝﹣19．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校有21名同学们参加某比赛，预赛成绩各不同，要取前11名参加决赛，小颖已经知道了自己的成绩，她想知道自己能否进入决赛，只需要再知道这21名同学成绩的（ ）
    A.最高分
    B.中位数
    C.极差
    D.平均数

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场将一款空调按标价的八折出售，仍可获利10%，若该空调的进价为2000元，则标价元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

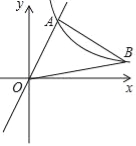
    【题目】如图，在平面直角坐标系中，经过点A的双曲线y=（x＞0）同时经过点B，且点A在点B的左侧，点A的横坐标为，∠AOB=∠OBA=45°，则k的值为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为创建全国文明城市，开展“美化绿化城市”活动，计划经过若干年使城区绿化总面积新增360万平方米．自2013年初开始实施后，实际每年绿化面积是原计划的1.6倍，这样可提前4年完成任务．

    （1）问实际每年绿化面积多少万平方米？

    （2）为加大创城力度，市政府决定从2016年起加快绿化速度，要求不超过2年完成，那么实际平均每年绿化面积至少还要增加多少万平方米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【操作发现】

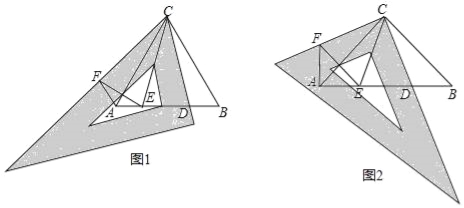
    （1）如图1，为等边三角形，先将三角板中的角与重合，再将三角板绕点按顺时针方向旋转（旋转角大于且小于）.旋转后三角板的一直角边与交于点.在三角板斜边上取一点，使，线段上取点，使，连接，.

    ①求的度数；

    ②与相等吗？请说明理由；

    【类比探究】

    （2）如图2，为等腰直角三角形，，先将三角板的角与重合，再将三角板绕点按顺时针方向旋转（旋转角大于且小于）.旋转后三角板的一直角边与交于点.在三角板另一直角边上取一点，使，线段上取点，使，连接，.请直接写出探究结果：

    ①的度数；

    ②线段之间的数量关系.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以下五个命题：①对顶角相等；②内错角相等；③同位角相等，两直线平行；④0的立方根是0；⑤无限不循环小数是无理数．其中真命题的个数为（ ）
    A.2
    B.3
    C.4
    D.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数（a是常数，a≠0），下列结论正确的是（ ）

    A．当a=1时，函数图象经过点（﹣1，1）

    B．当a=﹣2时，函数图象与x轴没有交点

    C．若a＜0，函数图象的顶点始终在x轴的下方

    D．若a＞0，则当x≥1时，y随x的增大而增大

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【感知】如图①，四边形ABCD、CEFG均为正方形．可知BE=DG． 【拓展】如图②，四边形ABCD、CEFG均为菱形，且∠A=∠F．求证：BE=DG．
    【应用】如图③，四边形ABCD、CEFG均为菱形，点E在边AD上，点G在AD延长线上．若AE=2ED，∠A=∠F，△EBC的面积为8，则菱形CEFG的面积为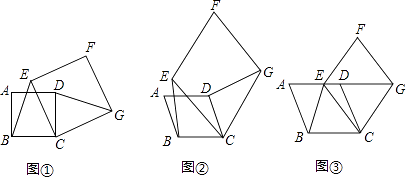

    查看答案和解析>>

    同步练习册答案