
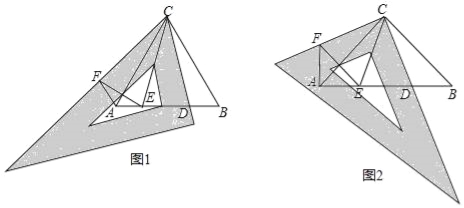
【题目】【操作发现】
(1)如图1,![]() 为等边三角形,先将三角板中的
为等边三角形,先将三角板中的![]() 角与
角与![]() 重合,再将三角板绕点
重合,再将三角板绕点![]() 按顺时针方向旋转(旋转角大于
按顺时针方向旋转(旋转角大于![]() 且小于
且小于![]() ).旋转后三角板的一直角边与
).旋转后三角板的一直角边与![]() 交于点
交于点![]() .在三角板斜边上取一点
.在三角板斜边上取一点![]() ,使
,使![]() ,线段
,线段![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() .
.
①求![]() 的度数;
的度数;
②![]() 与
与![]() 相等吗?请说明理由;
相等吗?请说明理由;
【类比探究】
(2)如图2,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,先将三角板的
,先将三角板的![]() 角与
角与![]() 重合,再将三角板绕点
重合,再将三角板绕点![]() 按顺时针方向旋转(旋转角大于
按顺时针方向旋转(旋转角大于![]() 且小于
且小于![]() ).旋转后三角板的一直角边与
).旋转后三角板的一直角边与![]() 交于点
交于点![]() .在三角板另一直角边上取一点
.在三角板另一直角边上取一点![]() ,使
,使![]() ,线段
,线段![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() .请直接写出探究结果:
.请直接写出探究结果:
①![]() 的度数;
的度数;
②线段![]() 之间的数量关系.
之间的数量关系.
【答案】(1)①120°;②DE=EF;理由见解析;(2)①90°;②AE2+DB2=DE2.理由见解析.
【解析】
试题分析:(1)①由等边三角形的性质得出AC=BC,∠BAC=∠B=60°,求出∠ACF=∠BCD,证明△ACF≌△BCD,得出∠CAF=∠B=60°,求出∠EAF=∠BAC+∠CAF=120°;
②证出∠DCE=∠FCE,由SAS证明△DCE≌△FCE,得出DE=EF即可;
(2)①由等腰直角三角形的性质得出AC=BC,∠BAC=∠B=45°,证出∠ACF=∠BCD,由SAS证明△ACF≌△BCD,得出∠CAF=∠B=45°,AF=DB,求出∠EAF=∠BAC+∠CAF=90°;
②证出∠DCE=∠FCE,由SAS证明△DCE≌△FCE,得出DE=EF;在Rt△AEF中,由勾股定理得出AE2+AF2=EF2,即可得出结论.
试题解析:(1)①∵△ABC是等边三角形,
∴AC=BC,∠BAC=∠B=60°,
∵∠DCF=60°,
∴∠ACF=∠BCD,
在△ACF和△BCD中,
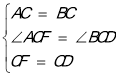 ,
,
∴△ACF≌△BCD(SAS),
∴∠CAF=∠B=60°,
∴∠EAF=∠BAC+∠CAF=120°;
②DE=EF;理由如下:
∵∠DCF=60°,∠DCE=30°,
∴∠FCE=60°﹣30°=30°,
∴∠DCE=∠FCE,
在△DCE和△FCE中,
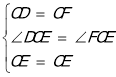 ,
,
∴△DCE≌△FCE(SAS),
∴DE=EF;
(2)①∵△ABC是等腰直角三角形,∠ACB=90°,
∴AC=BC,∠BAC=∠B=45°,
∵∠DCF=90°,
∴∠ACF=∠BCD,
在△ACF和△BCD中,
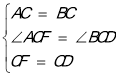 ,
,
∴△ACF≌△BCD(SAS),
∴∠CAF=∠B=45°,AF=DB,
∴∠EAF=∠BAC+∠CAF=90°;
②AE2+DB2=DE2,理由如下:
∵∠DCF=90°,∠DCE=45°,
∴∠FCE=90°﹣45°=45°,
∴∠DCE=∠FCE,
在△DCE和△FCE中,
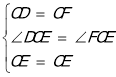 ,
,
∴△DCE≌△FCE(SAS),
∴DE=EF,
在Rt△AEF中,AE2+AF2=EF2,
又∵AF=DB,
∴AE2+DB2=DE2.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点.
例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P为△ABC的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点M是曲线C:![]()
![]() 上的任意一点,点N是x轴正半轴上的任意一点.
上的任意一点,点N是x轴正半轴上的任意一点.
(1) 如图2,点P是OM上一点,∠ONP=∠M, 试说明点P是△MON的自相似点; 当点M的坐标是![]() ,点N的坐标是
,点N的坐标是![]() 时,求点P 的坐标;
时,求点P 的坐标;
(2) 如图3,当点M的坐标是![]() ,点N的坐标是
,点N的坐标是![]() 时,求△MON的自相似点的坐标;
时,求△MON的自相似点的坐标;
(3) 是否存在点M和点N,使△MON无自相似点,?若存在,请直接写出这两点的坐标;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x,y为有理数,现规定一种新运算“〇”满足x〇y=y2﹣2x
(1)求5〇(﹣3);
(2)求(5〇x)﹣2(y〇x),其中|x﹣1|+(y+2)4=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com