
【题目】关于二次函数y=mx2+(2m+4)x+8(m为常数,且m≠0),
(1)证明:该函数与x轴一定有交点;
(2)若该函数经过点A(﹣1+![]() ,y1)B(﹣1,y2),请比较y1,y2的大小关系,并说明理由.
,y1)B(﹣1,y2),请比较y1,y2的大小关系,并说明理由.
【答案】(1)见解析;(2)当m>0时, y1>y2;当m<0时, y2>y1.
【解析】
(1)证得△=(2m+4)232m=(2m4)2≥0,则函数与x轴一定有交点;
(2)函数的对称轴为x=﹣1﹣![]() ,当m>0时,﹣1+
,当m>0时,﹣1+![]() >﹣1>﹣1﹣
>﹣1>﹣1﹣![]() ,y随x的增大而增大,所以y1>y2;当m<0时,﹣1﹣
,y随x的增大而增大,所以y1>y2;当m<0时,﹣1﹣![]() >﹣1>﹣1+
>﹣1>﹣1+![]() ,y随x的增大而增大,所以y2>y1;
,y随x的增大而增大,所以y2>y1;
(1)二次函数y=mx2+(2m+4)x+8,
△=(2m+4)2﹣32m=4m2﹣32m+16=(2m﹣4)2≥0,
∴函数与x轴一定有交点;
(2)函数的对称轴为x=﹣1﹣![]() ,
,
当m>0时,﹣1+![]() >﹣1>﹣1﹣
>﹣1>﹣1﹣![]() ,
,
∴y随x的增大而增大,
∴y1>y2;
当m<0时,﹣1﹣![]() >﹣1>﹣1+
>﹣1>﹣1+![]() ,
,
y随x的增大而增大,
∴y2>y1.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
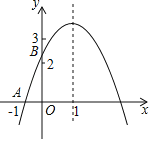
【题目】如图,二次函数y=ax2+bx+c(a≠0)图象与x轴交于A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(不包括这两个点),下列结论:
①当﹣1<x<3时,y>0;②﹣1<a<﹣![]() ;③当m≠1时,a+b>m(am+b);④4ac﹣b2>8a其中正确的结论是_____.
;③当m≠1时,a+b>m(am+b);④4ac﹣b2>8a其中正确的结论是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
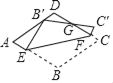
【题目】如图,在菱形紙片ABCD中,AB=2.将纸片折叠,使点B落在AD边上的点B′处(不与A,D重合),点C落在C′处,线段B′C′与直线CD交于点G,折痕为EF,则下列说法:①若∠A=90,B′为AD中点时,AE=![]() ;②若∠A=60°,B′为AD中点时,点E恰好是AB的中点;③若∠A=60°,C′F⊥CD时,
;②若∠A=60°,B′为AD中点时,点E恰好是AB的中点;③若∠A=60°,C′F⊥CD时,![]() ,其中正确的是( )
,其中正确的是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是等边△ABC内一点,将△DBC绕点B旋转到△EBA的位置,则∠EBD的度数是( )

A. 45°B. 60°C. 90°D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级数学模拟测试中,六名学生的数学成绩如下表所示,下列关于这组数据描述正确的是( )
姓名 | 小红 | 小明 | 小东 | 小亮 | 小丽 | 小华 |
成绩(分) | 110 | 106 | 109 | 111 | 108 | 110 |
A.众数是110B.方差是16
C.平均数是109.5D.中位数是109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,如图所示是小明从家到学校这一过程中所走的路程 s(米)与时间 t(分)之间的关系.
(1)小明从家到学校的路程共 米,从家出发到学校,小明共用了 分钟;
(2)小明修车用了多长时间?
(3)小明修车以前和修车后的平均速度分别是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣(a+1)x﹣3与x轴交于A、B两点,点A的坐标为(﹣1,0).
(1)求B点与顶点D的坐标;
(2)经过点B的直线l与y轴正半轴交于点M,S△ADM=5,求直线l的解析式;
(3)点P(t,0)为x轴上一动点,过点P作x轴的垂线m,将抛物线在直线m左侧的部分沿直线m对折,图象的其余部分保持不变,得到一个新图象G.请结合图象回答:当图象G与直线l没有公共点时,t的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com