
����Ŀ����ƽ��ֱ������ϵxOy�У�������y��ax2����a+1��x��3��x�ύ��A��B���㣬��A������Ϊ����1��0����
��1����B���붥��D�����ꣻ
��2��������B��ֱ��l��y�������ύ�ڵ�M��S��ADM��5����ֱ��l�Ľ���ʽ��
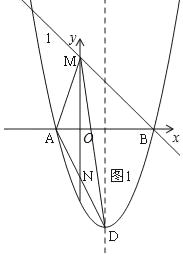
��3����P��t��0��Ϊx����һ���㣬����P��x��Ĵ���m������������ֱ��m���IJ�����ֱ��m���ۣ�ͼ������ಿ�ֱ��ֲ��䣬�õ�һ����ͼ��G������ͼ��ش𣺵�ͼ��G��ֱ��lû�й�����ʱ��t��ȡֵ��Χ���� ����
���𰸡���1��D��1����4����B��3��0������2��y����x+3����3��![]() ��
��
��������
��1���ѵ�A�����꣨-1��0������y=ax2-��a+1��x-3�У������a��ֵ���䷽��ɵö���D�����꣬�ɶԳ��Կɵõ�B�����ꣻ
��2�����������ε����=Ǧֱ�߶���ˮƽ���ȵĻ����е�ʽ���ɵ�OM�ij���д��M�����꣬���ô���ϵ������ֱ��l�Ľ���ʽ��
��3�����ݶ��۵����ʵ��������ߵĶ������꣬�ɿ�����ͬ��֪��a=1���ɵý���ʽ����ͼ��G��ֱ��lû�й�����ʱ����������ʽ�����������⣬�ɵý��ۣ�
�⣺��1���ѵ�A�����꣨��1��0������y��ax2����a+1��x��3�У�
�ã�a+��a+1����3��0��
a��1��
��y��x2��2x��3����x��1��2��4��
��D��1����4����
�ɶԳ��Եã�B��3��0����
��2����ֱ��AD�Ľ���ʽΪ��y��kx+b��
��![]() ��
��
��ã�![]() ��
��
��ֱ��AD�Ľ���ʽΪ��y����2x��2��
��AD��y����N��
��ON��2��
��S��ADM��![]() MN����xA+xD����5��
MN����xA+xD����5��
��![]() ��2+OM������1+1����5��
��2+OM������1+1����5��
OM��3��
��M��0��3����
��ֱ��l�Ľ���ʽΪ��y��kx+b��
��![]() ��
��
��ã�![]() ��
��
ֱ��l�Ľ���ʽΪ��y����x+3��
��3����ͼ2���ɶ��۵ã�OC��3+2��t��3��+2��2t��1��
���������ߵĶ���Ϊ��2t��1����4����
����ʽΪ��y����x��2t+1��2��4��
��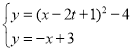 ��
��
��x��2t+1��2��4����x+3��
x2����4t��3��x+4t2��4t��6��0��
������0ʱ��ͼ��G��ֱ��lû�й����㣬
������[����4t��3��]2��4��4t2��4t��6����0��
t��![]() ��
��
�ʴ�Ϊ����


 ���ſ����ϵ�д�
���ſ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���y��mx2+��2m+4��x+8��mΪ��������m��0����
��1��֤�����ú�����x��һ���н��㣻
��2�����ú���������A����1+![]() ��y1��B����1��y2������Ƚ�y1��y2�Ĵ�С��ϵ����˵�����ɣ�
��y1��B����1��y2������Ƚ�y1��y2�Ĵ�С��ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
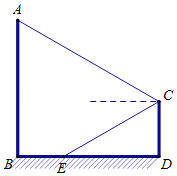
����Ŀ��ij���ֳ�һת�ǻ�����ͼ��ʾ����������AB��CD����ֱ�ڵ��棬��E���߶�BD�ϣ���C���õ�A������Ϊ30������E�ĸ���ҲΪ30�������B��E�����Ϊ10�ף�����AB��30�ף�������CD�ĸߣ�����������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ڵ����㳡��������ý���ע����������Ƶ��Ϊ�˽��й�ר�ñ�����Сƽ���˽ⱾС����������㳡�����Ŀ�����������һ�γ������飬�Ѿ�������㳡�����Ŀ�����Ϊ�ĸ���Σ�A���dz���ͬ��B����ͬ��Ҫ��ʱ�����ƣ�C������ν��D������ͬ������������������ͼ1��ͼ2������������ͳ��ͼ��

�������ͼ���ṩ����Ϣ����������⣺
��1���α����ľ����ж����ˣ�
��2����ͼ1��ͼ2����������
��3����ͼ2����C������������ε�Բ�ĽǵĶ�����
��4�����Ƹ�С��4000�������ж����㳡�����Ŀ�����ʾ��ͬ������A��κ�B��Σ��Ĵ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
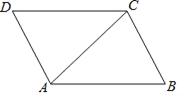
����Ŀ����ͼ��AC��ƽ���ı���ABCD�ĶԽ��ߣ�
��1�����ó߹�����AC�Ĵ�ֱƽ���ߣ�Ҫ������ͼ�ۼ�����д��������
��2����AC�Ĵ�ֱƽ���߷ֱ���AB��AC��CD���ڵ�E��O��F����֤����A��E��C��FΪ������ı���Ϊ���Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ƽ��ֱ������ϵxOy�У�������![]() ����ԭ�㣬����x���ཻ�ڵ�A����A�ĺ�����Ϊ6�������߶���Ϊ��B��
����ԭ�㣬����x���ཻ�ڵ�A����A�ĺ�����Ϊ6�������߶���Ϊ��B��
��1�������������ߵı���ʽ�Ͷ���B�����ꣻ
��2������O��OP��AB����ֱ��OP�ϵ�ȡһ��Q��ʹ�á�QAB=��OBA�����Q�����ꣻ
��3����������������ƽ��m��m��0������λ����������������y�Ḻ�����ཻ�ڵ�C�Ҷ�����Ȼ�ڵ������ޣ���ʱ��A�ƶ�����D��λ�ã�CB��DB=3��4����m��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
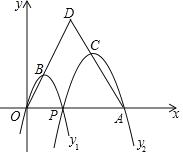
����Ŀ����ͼ����֪��A��4��0����OΪ����ԭ�㣬P���߶�OA������һ�㣨�����˵�O��A������P��O����Ķ��κ���y1��P��A����Ķ��κ���y2��ͼ�ھ����£����ǵĶ���ֱ�ΪB��C������OB������AC�ཻ�ڵ�D������ODA�ǵȱ�������ʱ�����������κ��������ֵ֮�͵���__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ı���ABCD�У�AD��BC��AD=CD��E�ǶԽ���BD��һ�㣬��EA=EC��
��1����֤���ı���ABCD�����Σ�
��2�����BE=BC������CBE����BCE=2��3����֤���ı���ABCD�������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵxOy�У�ֱ��l��x���y���ڵ�A����3��0����B��0��3����
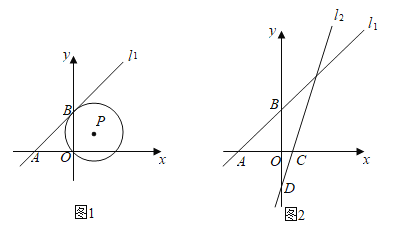
��1����ͼ1����֪��P������O������ֱ��l1�����ڵ�B�����P��ֱ������
��2����ͼ2����ֱ֪��l2��y��3x����x���y���ڵ�C�͵�D����Q��ֱ��l2�ϵ�һ�����㣬��QΪԲ�ģ�2![]() Ϊ�뾶��Բ��
Ϊ�뾶��Բ��
�ٵ���Q���C�غ�ʱ����֤��ֱ��l1���Q���У�
�����Q��ֱ��l1�ཻ��M��N���㣬����QM��QN���ʣ��Ƿ���������ĵ�Q��ʹ�á�QMN�ǵ���ֱ�������Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com