
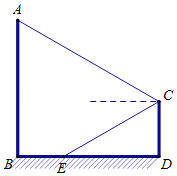
【题目】某游乐场一转角滑梯如图所示,滑梯立柱AB、CD均垂直于地面,点E在线段BD上,在C点测得点A的仰角为30°,点E的俯角也为30°,测得B、E间距离为10米,立柱AB高30米.求立柱CD的高(结果保留根号)
科目:初中数学 来源: 题型:
【题目】我们把有两条边和其中一边的对角对应相等的两个三角形叫做友好三角形。如图,在△ABC和△ABD中,AB=AB,AD=AC,∠ABC=∠ABD,则△ABC和△ABD是友好三角形。
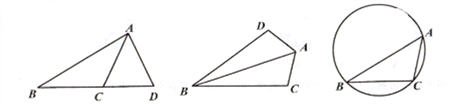
(1)如图1,已知AD=AC,请写出图中的友好三角形;
(2)如图2,在△ABC和△ABD中,AD=AC,∠BDA=∠BCA,且∠BDA>90°,
求证:△ABC≌△ABD;
(3) 如图3,△ABC内接于圆,∠ABC=30°,∠BAC=45°,BC=4。D是圆上一点,若△ABD和△ABC是友好三角形,且BD<AD,求AD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一种折叠门,由上下轨道和两扇长宽相等的活页门组成,整个活页门的右轴固定在门框
上,通过推动左侧活页门开关;图2是其俯视图简化示意图,已知轨道![]() ,两扇活页门的宽
,两扇活页门的宽![]() ,点
,点![]() 固定,当点
固定,当点![]() 在
在![]() 上左右运动时,
上左右运动时,![]() 与
与![]() 的长度不变(所有结果保留小数点后一位).
的长度不变(所有结果保留小数点后一位).
(1)若![]() ,求
,求![]() 的长;
的长;
(2)当点![]() 从点
从点![]() 向右运动60
向右运动60![]() 时,求点
时,求点![]() 在此过程中运动的路径长.
在此过程中运动的路径长.
(参考数据:sin50°≈0.77, cos50°≈0.64, tan50°≈1.19, π取3.14)

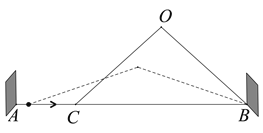
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】借助表格进行多项式乘多项式运算,可以方便合并同类项得出结果.下面尝试利用表格试一试.
例题:(a+b)(a﹣b)
解填表
| a | b |
a | a2 | ab |
﹣b | ﹣ab | ﹣b2 |
则(a+b)(a﹣b)=a2﹣b2.
根据所学完成下列问题.
(1)如表,填表计算(x+2)(x2﹣2x+4),(m+3)(m2﹣3m+9),直接写出结果.
| x2 | ﹣2x | 4 |
x | x3 | ﹣2x2 | 4x |
+2 | 2x2 | ﹣4x | 8 |
| m2 | ﹣3m | 9 |
m | m3 | ﹣3m2 | 9m |
+3 | 3m2 | ﹣9m | 27 |
结果为 ;结果为 .
(2)根据以上获得的经验填表:
| |||
△ | △3 | ||
〇 | 〇3 |
结果为△3+〇3,根据以上探索,请用字母a、b来表示发现的公式为 .
(3)用公式计算:(2x+3y)(4x2﹣6xy+9y2)= ;
因式分解:27m3﹣8n3= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按所选做的第一题计分,
(1)若![]() ,则
,则![]() ______
______
(2)钟面上6点20分时,时针与分针所构成的角的度数是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
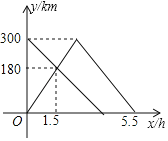
【题目】甲、乙两车分别从A,B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地.设甲、乙两车距A地的路程为y(km),甲车行驶的时间为x(h),y与x之间的关系图象如图所示:①甲车从A地到达B地的行驶时间为2h;②甲车返回时y与x之间的关系式是y=﹣100x+550;③甲车返回时用了3个小时;④乙车到达A地时甲车距A地的路程是170km.上述说法正确的有( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
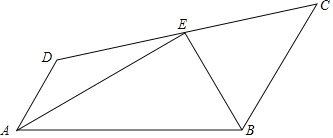
【题目】如图,四边形ABCD中,AD∥BC,点E在CD上,EA,EB分别平分∠DAB和∠CBA,设AD=x,BC=y且(x﹣3)2+|y﹣4|=0.求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明买了张100元的乘车IC卡,如果他乘车的次数用x表示,则记录他每次乘车后的余额y元)如表:
次数x | 1 | 2 | 3 | 4 | … |
余额y | 100-1.2 | 100-2.4 | 100-3.6 | 100-4.8 | … |
(1)写出乘车的次数x表示余额y的关系式.
(2)利用上述关系式计算小明乘了15次车还剩下多少元?
(3)余额还有40元时,小明已使用此卡乘车多少次?
(4)小强最多能乘几次车?
查看答案和解析>>
科目:初中数学 来源: 题型:
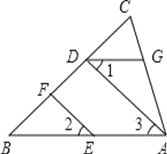
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
∵EF∥AD,(________)
∴∠2=______.(两直线平行,同位角相等;)
又∵∠1=∠2,(________)
∴∠1=∠3.(________)
∴AB∥DG.(________)
∴∠BAC+______=180°(________)
又∵∠BAC=70°,(________)
∴∠AGD=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com