【题目】请从以下两个小题中任选一个作答，若多选，则按所选做的第一题计分，
（1）若
，则
______
（2）钟面上6点20分时，时针与分针所构成的角的度数是______度．
【答案】1 70
【解析】
（1）根据mn=m+3，先化简2mn+3m-5mn+10，再求出算式的值是多少即可．
（2）因为钟表上的刻度是把一个圆平均分成了12等份，每一份是30
，借助图形，找出6点20分时针和分针之间相差的大格数，用大格数乘30即可．
解：
（1）∵mn=m+3，
∴2mn+3m5mn+10=3m3mn+10=3m3(m+3)+10=3m3m9+10=1；
（2）时针在钟面上每分钟转0.5，分针每分钟转6，
钟表上6时20分钟时，时针与分针的夹角可以看成时针转过6时0.5×20=10，分针在数字4上，
钟表12个数字，每相邻两个数字之间的夹角为30，
6时20分钟时分针与时针的夹角2×30+10=70，
故在6点20分，时针和分针的夹角为70；
故答案为：（1）1；（2）70.
科目：初中数学 来源： 题型：
【题目】请仔细阅读下面两则材料，然后解决问题：
材料1：小学时我们学过，任何一个假分数都可以化为一个整数与一个真分数的和的形式，同样道理，任何一个分子次数不低于分母次数的分式都可以化为一个整式与另一个分式的和（或差）的形式，其中分式的分子次数低于分母次数.
如：
.
材料2：对于式子
，利用换元法，令
，
.则由于
，所以反比例函数有最大值，且为3.因此分式的最大值为5.
根据上述材料，解决下列问题：
（1）把分式
化为一个整式与另一个分式的和的形式，其中分式的分子次数低于分母次数.
（2）当
的值变化时，求分式
的最大（或最小）值.
查看答案和解析>>
科目：初中数学 来源： 题型：
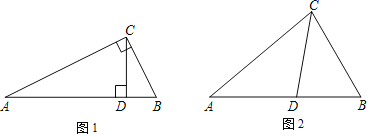
【题目】概念学习
规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．
从三角形
不是等腰三角形
一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．
理解概念
如图1，在
中，
，
，请写出图中两对“等角三角形”
概念应用
如图2，在
中，CD为角平分线，
，
．
求证：CD为的等角分割线．
在中，
，CD是的等角分割线，直接写出
的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
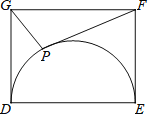
【题目】在△ABC中，若O为BC边的中点，则必有：AB2+AC2=2AO2+2BO2成立．依据以上结论，解决如下问题：如图，在矩形DEFG中，已知DE=4，EF=3，点P在以DE为直径的半圆上运动，则PF2+PG2的最小值为（ ）
A. 
B. 
C. 34 D. 10
查看答案和解析>>
科目：初中数学 来源： 题型：
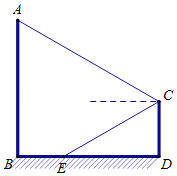
【题目】某游乐场一转角滑梯如图所示，滑梯立柱AB、CD均垂直于地面，点E在线段BD上，在C点测得点A的仰角为30°，点E的俯角也为30°，测得B、E间距离为10米，立柱AB高30米．求立柱CD的高（结果保留根号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明家1至6月份的用水量统计如图所示，关于这组数据，下列说法错误的是（ ）．
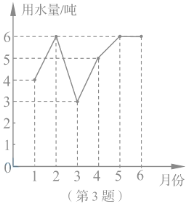
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图,点D在等边△ABC的边AB上，作DG∥BC，交AC于点G，点F在边AC上，连接DF并延长，交BC的延长线于点E，FE=FD.求证：AD=CE.
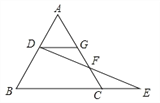
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=AC，利用直尺和圆规完成如下操作：
①作∠BAC的平分线交BC于点D；
②作边AB的垂直平分线EF，EF与AD相交于P点；
③连接PB、PC，
请你观察所作图形，解答下列问题：
（1）线段PA、PB、PC之间的大小关系是________；
（2）若∠ABC=68°，求∠BPC的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
