
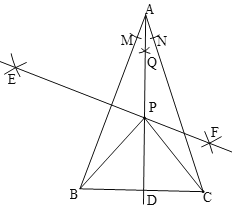
【题目】如图,△ABC中,AB=AC,利用直尺和圆规完成如下操作:
①作∠BAC的平分线交BC于点D;
②作边AB的垂直平分线EF,EF与AD相交于P点;
③连接PB、PC,
请你观察所作图形,解答下列问题:

(1)线段PA、PB、PC之间的大小关系是________;
(2)若∠ABC=68°,求∠BPC的度数.
【答案】(1)![]() ;(2)88°.
;(2)88°.
【解析】
根据角平分线的作法、线段垂直平分线的作法作出AD、EF即可;
(1)根据等腰三角形“三线合一”的性质可得直线AD是线段BC的垂直平分线,根据垂直平分线的性质可得PA=PB=PC;
(2)根据等腰三角形的性质可得∠ACB=∠ABC=68°,
①以A为圆心,任意长为半径画弧,交AB、AC于M、N,分别以M、N为圆心,大于![]() MN长为半径画弧,两弧交于点Q,作射线AQ,交BC于D;
MN长为半径画弧,两弧交于点Q,作射线AQ,交BC于D;
②分别以A、B为圆心,大于![]() AB长为半径画弧,两弧交于E、F,作直线EF交AD于P,
AB长为半径画弧,两弧交于E、F,作直线EF交AD于P,
③连接PB、PC,
∴如图即为所求,
(1)∵AD是∠BAC的角平分线,AB=AC,
∴AD是BC的垂直平分线,
∴PB=PC,
∵EF是AB的垂直平分线,
∴PA=PB,
∴PA=PB=PC,
故答案为:PA=PB=PC
(2)∵AB=AC,∠ABC=68°,
∴![]() ,
,
∴∠BAC=180°-2×68°=44°,
∵AD平分∠BAC,
∴∠BAD=∠CAD=22°,
由(1)可知PA=PB=PC,
∴∠PBA=∠PAB=∠PCA=22°
∴∠BPD=∠CPD=2∠PAB=44°,
∴∠BPC=2∠BPD=88°,


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按所选做的第一题计分,
(1)若![]() ,则
,则![]() ______
______
(2)钟面上6点20分时,时针与分针所构成的角的度数是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.

(1)求点B的坐标;
(2)求直线BC的解析式;
(3)直线EF:y=2x-k(k≠0)交AB于E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使得S△EBD=S△FBD?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小明从学校到家里行进的路程![]() (米)与时间
(米)与时间![]() (分)的函数图象.给出以下结论:①学校离小明家
(分)的函数图象.给出以下结论:①学校离小明家![]() 米;②小明用了
米;②小明用了![]() 分钟到家;③小明前
分钟到家;③小明前![]() 分钟走了整个路程的一半;④小明后
分钟走了整个路程的一半;④小明后![]() 分钟比前
分钟比前![]() 分钟走得快.其中正确结论的个数是( )
分钟走得快.其中正确结论的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10,正方形A、B、C、D的面积之和为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
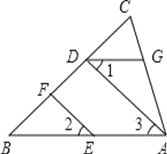
∵EF∥AD,(________)
∴∠2=______.(两直线平行,同位角相等;)
又∵∠1=∠2,(________)
∴∠1=∠3.(________)
∴AB∥DG.(________)
∴∠BAC+______=180°(________)
又∵∠BAC=70°,(________)
∴∠AGD=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的底边BC长为4,面积为16,腰AC的垂直平分线EF分别交AC、AB边于E、F两点,若D为BC边中点,点M为线段EF上一动点,则△CDM周长的最小值为 ( )

A. 6 B. 8 C. 12 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com