
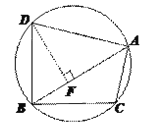
【题目】我们把有两条边和其中一边的对角对应相等的两个三角形叫做友好三角形。如图,在△ABC和△ABD中,AB=AB,AD=AC,∠ABC=∠ABD,则△ABC和△ABD是友好三角形。
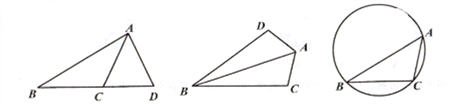
(1)如图1,已知AD=AC,请写出图中的友好三角形;
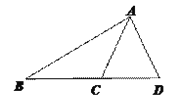
(2)如图2,在△ABC和△ABD中,AD=AC,∠BDA=∠BCA,且∠BDA>90°,
求证:△ABC≌△ABD;
(3) 如图3,△ABC内接于圆,∠ABC=30°,∠BAC=45°,BC=4。D是圆上一点,若△ABD和△ABC是友好三角形,且BD<AD,求AD的长。
【答案】(1)△ABC和△ABD (2)见解析 (3)![]()
【解析】(1)根据友好三角形的概念判断即可;(2)连结CD,由等腰三角形的性质得出∠ADC=∠ACD,再由∠ADB=∠ACB,根据等量代换推出∠BDC=∠BCD,继而得出BD=CD,利用SSS即可得证;(3)分三种情况讨论:① 当AB=AB,AD=BC时;② 当AB=AB,DB=AC时;③ 当AB=AB,BD=BC时去分析求解.
(1):如图, △ABC和△ABD
(2):连结CD,
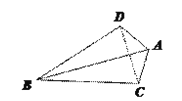
∵AD=AC, ∴∠ADC=∠ACD
∵∠ADB=∠ACB,
∴![]() ,即
,即![]()
∴BD=CD
∵AB=AB, ∴ △ABC≌△ABD (SSS)
(3)① 如图,当![]() 时,
时,![]() ,
,
△ABD和△ABC是友好三角形. ∴AD =4
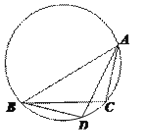
② 如图,当![]() 时,
时,![]() ,
,
△ABD和△ABC是友好三角形.
过C作CE⊥AB于点E
∵![]() ,BC=4, ∴
,BC=4, ∴ ![]()
∵![]() , ∴
, ∴![]()
∴![]()
∵![]() , ∴
, ∴![]()
∴![]() ,即
,即![]()
∴![]()

③ 如图9,当![]() 时,
时,![]() ,
,
△ABD和△ABC是友好三角形.
过D作DF⊥BA于点F
∵![]() ∴
∴![]() ,
,![]()
∴![]() , ∴
, ∴![]()
∴![]()
综上所述:AD的长度为![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】某学校计划购买一批课外读物,为了了解学生对课外读物的需求情况,学校进行了一次“我最喜爱的课外读物”的调查,设置了“文学”、“科普”、“艺术”和“其他”四个类别,规定每人必须并且只能选择其中一类,现从全体学生的调查表中随机抽取了部分学生的调查表进行统计,并把统计结果绘制了如图所示的两幅不完整的统计图.
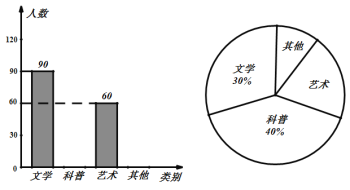
(1) 从全体学生的调查表中随机抽取了多少名学生?
(2) 将条形图补充完整;
(3) 艺术类读物所在扇形的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
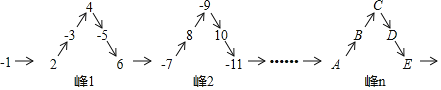
【题目】将一列有理数﹣1,2,﹣3,4,﹣5,6,…如图所示有序排列,根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰6”中C的位置是有理数_____,﹣2019应排在A、B、C、D、E中的_____位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种盛酒的桶,已知10个大桶加上2个小桶可以盛酒6斛(斛,音hu,是古代的一种容量单位),3个大桶加上15个小桶也可以盛酒6斛.
(1)求1个大桶可盛酒多少斛?
(2)分析2个大桶加上3个小桶可以盛酒2斛吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请仔细阅读下面两则材料,然后解决问题:
材料1:小学时我们学过,任何一个假分数都可以化为一个整数与一个真分数的和的形式,同样道理,任何一个分子次数不低于分母次数的分式都可以化为一个整式与另一个分式的和(或差)的形式,其中分式的分子次数低于分母次数.
如:![]() .
.
材料2:对于式子![]() ,利用换元法,令
,利用换元法,令![]() ,
,![]() .则由于
.则由于![]() ,所以反比例函数
,所以反比例函数![]() 有最大值,且为3.因此分式
有最大值,且为3.因此分式![]() 的最大值为5.
的最大值为5.
根据上述材料,解决下列问题:
(1)把分式![]() 化为一个整式与另一个分式的和的形式,其中分式的分子次数低于分母次数.
化为一个整式与另一个分式的和的形式,其中分式的分子次数低于分母次数.
(2)当![]() 的值变化时,求分式
的值变化时,求分式![]() 的最大(或最小)值.
的最大(或最小)值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() .
.
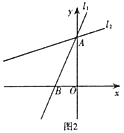
(1)求证:![]() .
.
(2)已知直线![]() 与
与![]() 轴交于
轴交于![]() 点,将直线
点,将直线![]() 绕着
绕着![]() 点顺时针旋转45°至
点顺时针旋转45°至![]() ,如图2,求
,如图2,求![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个能被13整除的自然数我们称为“十三数”,“十三数”的特征是:若把这个自然数的末三位与末三位以前的数字组成的数之差,如果能被13整除,那么这个自然数就一定能被13整除.例如:判断383357能不能被13整除,这个数的末三位数字是357,末三位以前的数字组成的数是383,这两个数的差是383﹣357=26,26能被13整除,因此383357是“十三数”.
(1)判断3253和254514是否为“十三数”,请说明理由.
(2)若一个四位自然数,千位数字和十位数字相同,百位数字与个位数字相同,则称这个四位数为“间同数”.
①求证:任意一个四位“间同数”能被101整除.
②若一个四位自然数既是“十三数”,又是“间同数”,求满足条件的所有四位数的最大值与最小值之差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场一转角滑梯如图所示,滑梯立柱AB、CD均垂直于地面,点E在线段BD上,在C点测得点A的仰角为30°,点E的俯角也为30°,测得B、E间距离为10米,立柱AB高30米.求立柱CD的高(结果保留根号)
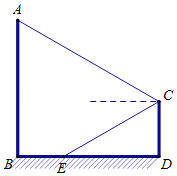
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com