
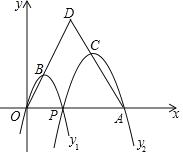
【题目】如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P,O两点的二次函数y1和过P,A两点的二次函数y2的图象开口均向下,它们的顶点分别为B,C,射线OB与射线AC相交于点D.当△ODA是等边三角形时,这两个二次函数的最大值之和等于__.
科目:初中数学 来源: 题型:
【题目】某校九年级数学模拟测试中,六名学生的数学成绩如下表所示,下列关于这组数据描述正确的是( )
姓名 | 小红 | 小明 | 小东 | 小亮 | 小丽 | 小华 |
成绩(分) | 110 | 106 | 109 | 111 | 108 | 110 |
A.众数是110B.方差是16
C.平均数是109.5D.中位数是109
查看答案和解析>>
科目:初中数学 来源: 题型:
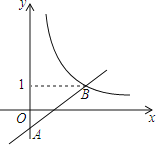
【题目】如图,在平面直角坐标系xOy中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A,与函数![]() (x>0)的图象相交于点B(t,1).
(x>0)的图象相交于点B(t,1).
(1)求点B的坐标及一次函数的解析式;
(2)点P的坐标为(m,m)(m>0),过P作PE∥x轴,交直线AB于点E,作PF∥y轴,交函数![]() (x>0)的图象于点F.
(x>0)的图象于点F.
①若m=2,比较线段PE,PF的大小;
②直接写出使PE≤PF的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣(a+1)x﹣3与x轴交于A、B两点,点A的坐标为(﹣1,0).
(1)求B点与顶点D的坐标;
(2)经过点B的直线l与y轴正半轴交于点M,S△ADM=5,求直线l的解析式;
(3)点P(t,0)为x轴上一动点,过点P作x轴的垂线m,将抛物线在直线m左侧的部分沿直线m对折,图象的其余部分保持不变,得到一个新图象G.请结合图象回答:当图象G与直线l没有公共点时,t的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
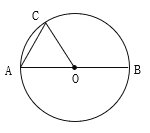
【题目】如图,在⊙O中,AB是直径,半径为R,弧AC=![]() R.
R.
求:(1)∠AOC的度数.(2)若D为劣弧BC上的一动点,且弦AD与半径OC交于E点.试探求△AEC≌△DEO时,D点的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
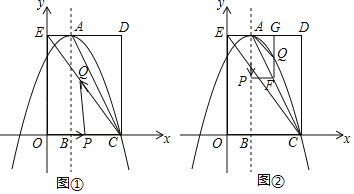
(1)求抛物线的解析式.
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划购买A型和B型课桌凳共200套,经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,,且购买4套A型和6套B型课桌凳共需1820元。
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳的![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
(1)求证:四边形AMCN是平行四边形;
(2)若AC=BC=5,AB=6,求四边形AMCM的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com