
【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
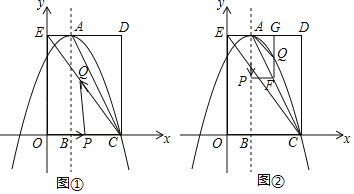
(1)求抛物线的解析式.
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
【答案】(1)y=﹣x2+2x+3;(2)当t=![]() 或t=
或t=![]() 时,△PCQ为直角三角形;(3)当t=2时,△ACQ的面积最大,最大值是1.
时,△PCQ为直角三角形;(3)当t=2时,△ACQ的面积最大,最大值是1.
【解析】
(1)根据抛物线的对称轴与矩形的性质可得点A的坐标,根据待定系数法可得抛物线的解析式;
(2)先根据勾股定理可得CE,再分两种情况:当∠QPC=90°时;当∠PQC=90°时;讨论可得△PCQ为直角三角形时t的值;
(3)根据待定系数法可得直线AC的解析式,根据S△ACQ=S△AFQ+S△CPQ可得S△ACQ=![]() =﹣
=﹣![]() (t﹣2)2+1,依此即可求解.
(t﹣2)2+1,依此即可求解.
解:(1)∵抛物线的对称轴为x=1,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4),点A在DE上,
∴点A坐标为(1,4),
设抛物线的解析式为y=a(x﹣1)2+4,把C(3,0)代入抛物线的解析式,可得a(3﹣1)2+4=0,解得a=﹣1.
故抛物线的解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3;
(2)依题意有:OC=3,OE=4,
∴CE=![]() =
=![]() =5,
=5,
当∠QPC=90°时,
∵cos∠QPC=![]() ,
,
∴![]() ,解得t=
,解得t=![]() ;
;
当∠PQC=90°时,
∵cos∠QCP=![]() ,
,
∴![]() ,解得t=
,解得t=![]() .
.
∴当t=![]() 或 t=
或 t=![]() 时,△PCQ为直角三角形;
时,△PCQ为直角三角形;
(3)∵A(1,4),C(3,0),
设直线AC的解析式为y=kx+b,则有:
![]() ,解得
,解得![]() .故直线AC的解析式为y=﹣2x+6.
.故直线AC的解析式为y=﹣2x+6.
∵P(1,4﹣t),将y=4﹣t代入y=﹣2x+6中,得x=1+![]() ,
,
∴Q点的横坐标为1+![]() ,将x=1+
,将x=1+![]() 代入y=﹣(x﹣1)2+4 中,得y=4﹣
代入y=﹣(x﹣1)2+4 中,得y=4﹣![]() .
.
∴Q点的纵坐标为4﹣![]() ,
,
∴QF=(4﹣![]() )﹣(4﹣t)=t﹣
)﹣(4﹣t)=t﹣![]() ,
,
∴S△ACQ =S△AFQ +S△CFQ
=![]() FQAG+
FQAG+![]() FQDG,
FQDG,
=![]() FQ(AG+DG),
FQ(AG+DG),
=![]() FQAD,
FQAD,
=![]() ×2(t﹣
×2(t﹣![]() ),
),
=﹣![]() (t﹣2)2+1,
(t﹣2)2+1,
∴当t=2时,△ACQ的面积最大,最大值是1.


科目:初中数学 来源: 题型:
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.

请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,抛物线![]() 经过原点,且与x轴相交于点A,点A的横坐标为6,抛物线顶点为点B.
经过原点,且与x轴相交于点A,点A的横坐标为6,抛物线顶点为点B.
(1)求这条抛物线的表达式和顶点B的坐标;
(2)过点O作OP∥AB,在直线OP上点取一点Q,使得∠QAB=∠OBA,求点Q的坐标;
(3)将该抛物线向左平移m(m>0)个单位,所得新抛物线与y轴负半轴相交于点C且顶点仍然在第四象限,此时点A移动到点D的位置,CB:DB=3:4,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P,O两点的二次函数y1和过P,A两点的二次函数y2的图象开口均向下,它们的顶点分别为B,C,射线OB与射线AC相交于点D.当△ODA是等边三角形时,这两个二次函数的最大值之和等于__.
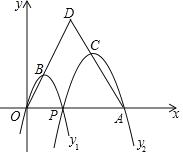
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为![]() 米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)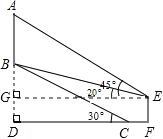
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】y=﹣2x+4直线交x轴于点A,交y轴于点B,抛物线y=﹣![]() (x﹣m)(x﹣6)(m>0)经过点A,交x轴于另一点C,如图所示.
(x﹣m)(x﹣6)(m>0)经过点A,交x轴于另一点C,如图所示.
(1)求抛物线的解析式.
(2)设抛物线的顶点为D,连接BD,AD,CD,动点P在BD上以每秒2个单位长度的速度由点B向点D运动,同时动点Q在线段CA上以每秒3个单位长度的速度由点C向点A运动,当其中一个点到达终点停止运动时,另一个点也随之停止运动,设运动时间为t秒.PQ交线段AD于点E.
①当∠DPE=∠CAD时,求t的值;
②过点E作EM⊥BD,垂足为点M,过点P作PN⊥BD交线段AB或AD于点N,当PN=EM时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB= 90° ,直角边AO在x轴上,且AO= 1.将 Rt△AOB绕原点O顺时针旋转90° 得到等腰直角三角形A1OB1,且A1O= 2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2,且A2O=2A1O......依此规律,得到等腰直角三角形A2018OB2018 ,则点A2018的坐标为__________.
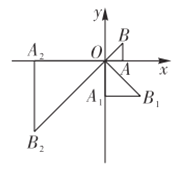
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com