
【题目】已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
(1)求证:四边形AMCN是平行四边形;
(2)若AC=BC=5,AB=6,求四边形AMCM的面积.

【答案】(1)见解析;(2)12.
【解析】
(1)由题意可得AB∥CD,AB=CD,又由M,N分别是AB和CD的中点可得AM=∥CN,即可得结论;
(2)根据等腰三角形的性质可得CM⊥AB,AM=3,根据勾股定理可得CM=4,则可求面积.
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵M,N分别为AB和CD的中点,
∴AM=![]() AB,CN=
AB,CN=![]() CD,
CD,
∴AM=CN,且AB∥CD,
∴四边形AMCN是平行四边形;
(2)∵AC=BC=5,AB=6,M是AB中点,
∴AM=MB=3,CM⊥AM,
∴CM=![]() ,
,
∵四边形AMCN是平行四边形,且CM⊥SM,
∴AMCN是矩形,
∴S四边形AMCN=12.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】学校实施新课程改革以来,学生的学习能力有了很大提高,王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图①②).请根据统计图解答下列问题:
(1)本次调查中,王老师一共调查了________名学生;
(2)将条形统计图补充完整;
(3)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:
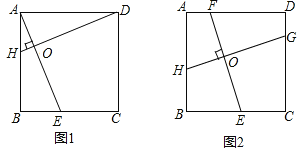
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
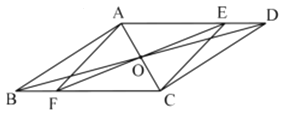
【题目】如图 ,在平行四边形 ABCD 中,对角线 AC 、 BD 交于点 O ,并且 DAC 60 ,ADB 15 ,点 E 是 AD 上一动点,延长 EO 交 BC 于点 F 。当点 E 从 D 点向 A 点移动 过程中(点 E 与点 D 、点 A 不重合),则四边形 AFCE 的变化是( )
A.平行四边形→矩形→平行四边形→菱形→平行四边形
B.平行四边形→矩形→平行四边形→正方形→平行四边形
C.平行四边形→菱形→平行四边形→矩形→平行四边形
D.平行四边形→矩形→菱形→正方形→平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形三个内角的度数之和是180°,如图是两个三角板不同位置的摆放,其中∠ACB=∠CDE=90°,∠BAC=60°,∠DEC=45°.
(1)当AB∥CD时,如图①,求∠DCB的度数;
(2)当CD与CB重合时,如图②,判断DE与AC的位置关系并说明理由;
(3)如图③,当∠DCB= 时,AB∥CE.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下表,回答问题:
x | … | -2 | -1 | 0 | 1 | 2 | … |
-2x+5 | … | 9 | 7 | 5 | 3 | a | … |
2x+8 | … | 4 | 6 | 8 | 10 | b | … |
(初步感知)
(1)a= ;b= ;
(归纳规律)
(2)随着x值的变化,两个代数式的值变化规律是什么?
(问题解决)
(3)比较-2x+5与2x+8的大小;
(4)请写出一个含x的代数式,要求x的值每增加1,代数式的值减小5,当x=0时,
代数式的值为-7.
查看答案和解析>>
科目:初中数学 来源: 题型:
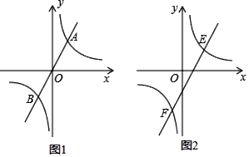
【题目】直线y=mx(m为常数)与双曲线y=![]() (k为常数)相交于A、B两点.
(k为常数)相交于A、B两点.
(1)若点A的横坐标为3,点B的纵坐标为﹣4
①直接写出:k=____,m=____;
②点C在第一象限内是双曲线y=![]() 的点,当S△OAC=9时,求点C的坐标;
的点,当S△OAC=9时,求点C的坐标;
(2)将直线y=mx向右平移得到直线y=mx+b,交双曲线y=![]() 于点E(4,y1)和F(﹣2,y2),直接写出不等式mx2+bx<k的解集:_____.
于点E(4,y1)和F(﹣2,y2),直接写出不等式mx2+bx<k的解集:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】莹莹家里今年种植的猕猴桃获得大丰收,星期六从外地来了一位客商到村子里收购猕猴桃.莹莹家卖给了该客商10箱猕猴桃.莹莹在家里帮助爸爸记账,每标准箱猕猴桃的净重为5千克,超过标准数的部分记为“+”,不足标准数的部分记为“﹣”,莹莹的记录如下:+0.4、+0.6、﹣0.2、+0.1、﹣0.6、﹣0.3、+0.4、0、+0.7、﹣0.3.
(1)请计算这10箱猕猴桃的总重为多少千克?
(2)如果弥猴桃的价格为9元/千克,莹莹家出售这10箱猕猴桃共收入多少元?(精确到1元)
(3)若都用这种纸箱装,莹莹家的猕猴桃共能装约2000箱,按照目前这个价格,把猕猴桃全部出售,莹莹家大约能收入多少元?(精确到万位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佳佳想探究一元三次方程x3+2x2-x-2=0的解的情况.根据以往的学习经验他想到了方程与函数的关系:一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一次方程kx+b=0(k≠0)的解;二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解.如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为方程x2-2x-3=0的解.
根据以上方程与函数的关系,若知道函数y=x3+2x2-x-2的图象与x轴交点的横坐标,即可知道方程x3+2x2-x-2=0的解.
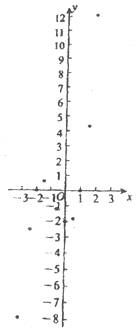
佳佳为了解函数y=x3+2x2-x-2的图象,通过描点法画出函数的图象:

(1)直接写出m的值________,并画出函数图象;
(2)根据表格和图象可知,方程的解有________个,分别为________________;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com