
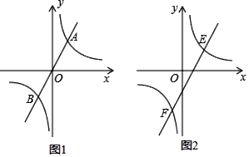
【题目】直线y=mx(m为常数)与双曲线y=![]() (k为常数)相交于A、B两点.
(k为常数)相交于A、B两点.
(1)若点A的横坐标为3,点B的纵坐标为﹣4
①直接写出:k=____,m=____;
②点C在第一象限内是双曲线y=![]() 的点,当S△OAC=9时,求点C的坐标;
的点,当S△OAC=9时,求点C的坐标;
(2)将直线y=mx向右平移得到直线y=mx+b,交双曲线y=![]() 于点E(4,y1)和F(﹣2,y2),直接写出不等式mx2+bx<k的解集:_____.
于点E(4,y1)和F(﹣2,y2),直接写出不等式mx2+bx<k的解集:_____.
【答案】(1)①12,![]() ;②点C的坐标为(6,2)或(
;②点C的坐标为(6,2)或(![]() ,8);(2)﹣2<x<4.
,8);(2)﹣2<x<4.
【解析】
(1)①根据正比例函数与双曲线的交点关于原点对称得出A(3,4),B(-3,-4),进而得出k=3×4=12,m=![]() ;
;
②如图,过A点作AM⊥x轴于点M,过C点作CN⊥x轴于点N,设C(x,![]() ),x>0.利用反比例函数比例系数k的几何意义得出S△ONC=S△OAM,再推出S△OAC=S梯形AMNC=9,根据梯形的面积公式列式计算即可;
),x>0.利用反比例函数比例系数k的几何意义得出S△ONC=S△OAM,再推出S△OAC=S梯形AMNC=9,根据梯形的面积公式列式计算即可;
(2)由双曲线y=![]() 过点E(4,y1)和F(-2,y2),得出E(4,
过点E(4,y1)和F(-2,y2),得出E(4,![]() ),F(-2,-
),F(-2,-![]() ),将E、F两点的坐标代入y=mx+b,得到
),将E、F两点的坐标代入y=mx+b,得到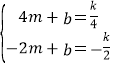 ,解得
,解得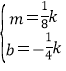 ,进而解不等式mx2+bx<k即可.
,进而解不等式mx2+bx<k即可.
(1) ①∵直线y=mx(m为常数)与双曲线y=![]() (k为常数)相交于A、B两点,点A的横坐标为3,点B的纵坐标为-4,
(k为常数)相交于A、B两点,点A的横坐标为3,点B的纵坐标为-4,
∴A(3,4),B(-3,-4),
∴k=3×4=12,m=![]() ;
;
②如图,过A点作AM⊥x轴于点M,过C点作CN⊥x轴于点N,设C(x,![]() ),x>0.
),x>0.
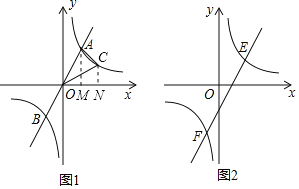
∵S△OAC+S△ONC=S梯形AMNC+S△OAM,S△ONC=S△OAM,
∴S△OAC=S梯形AMNC=9,
∴S梯形AMNC=![]() (AM+CN)MN=
(AM+CN)MN=![]() (4+
(4+![]() )|x﹣3|=9,
)|x﹣3|=9,
当x>3时,化简整理方程,得2x2﹣9x﹣18=0,解得x1=6,x2=﹣![]() (舍去),此时C
(舍去),此时C
(6,2);
当x<3时,化简整理方程,得2x2+9x﹣18=0,解得x1=﹣6(舍去),x2=![]() ,此时C(
,此时C(![]() ,8);
,8);
综上所述,所求点C的坐标为(6,2)或(![]() ,8);
,8);
(2) 将直线y=mx向右平移得到直线y=mx+b.
∵双曲线y=![]() 过点E(4,y1)和F(-2,y2),
过点E(4,y1)和F(-2,y2),
∴E(4,![]() ),F(-2,-
),F(-2,-![]() ),
),
∵直线y=mx+b过点E、F,
∴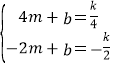 ,解得
,解得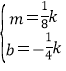 ,
,
∴不等式mx2+bx<k即为![]() kx2-
kx2-![]() kx<k,
kx<k,
∵k≠0,
∴x2-2x<8,
∴x2-2x-8<0,
∴-2<x<4.
故答案为:﹣2<x<4.


科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发去看望B,C,D格点处的其他甲虫,规定:向上向右走均为正,向下向左走均为负,如果从A到B记为A→B![]() 从B到A记为B→A
从B到A记为B→A![]() 其中第一个数表示左右方向移动,第二个数表示上下方向移动.
其中第一个数表示左右方向移动,第二个数表示上下方向移动.

(1)图中A→C![]() C→D
C→D![]()
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若图中格点处另有两只甲虫M,N.且M→A![]() M→N
M→N![]() ,则N→A应记为什么?直接写出答案.
,则N→A应记为什么?直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从有关方面获悉,在我市农村已经实行了农民新型合作医疗保险制度.享受医保的农民可在规定的医院就医并按规定标准报销部分医疗费用.下表是医疗费用报销的标准:
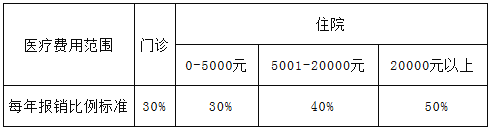
(说明:住院医疗费用为整数,住院医疗费用的报销分段计算.如:某人住院医疗费用共30000元,则5000元按30%报销、15000元按40%报销、余下的10000元按50%报销;题中涉及到的医疗费均指允许报销的医疗费)
(1)甲农民一年内实际门诊医疗费为2000元,则标准报销的金额为 元;
乙农民一年住院医疗费为15000元,则按标准报销的金额为 元;
(2)设某农民一年中住院的实际医疗费用为x元(5001≤x≤20000),按标准报销的金额为多少元?(用含x的代数式表示)
(3)若某农民一年内本人自负住院医疗费17000元(自负医疗费=实际医疗费﹣按标准报销的金额),则该农民当年实际医疗费用共多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
(1)求证:四边形AMCN是平行四边形;
(2)若AC=BC=5,AB=6,求四边形AMCM的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个问题解决往往经历发现猜想——探索归纳——问题解决的过程,下面结合一道几何题来体验一下.
(发现猜想)(1)如图①,已知∠AOB=70°,∠AOD=100°,OC为∠BOD的角平分线,则∠AOC的度数为 ;.


(探索归纳)(2)如图①,∠AOB=m,∠AOD=n,OC为∠BOD的角平分线. 猜想∠AOC的度数(用含m、n的代数式表示),并说明理由.
(问题解决)(3)如图②,若∠AOB=20°,∠AOC=90°,∠AOD=120°.若射线OB绕点O以每秒20°逆时针旋转,射线OC绕点O以每秒10°顺时针旋转,射线OD绕点O每秒30°顺时针旋转,三条射线同时旋转,当一条射线与直线OA重合时,三条射线同时停止运动. 运动几秒时,其中一条射线是另外两条射线夹角的角平分线?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为300,测得大楼顶端 A的仰角为450(点B,C,E在同一水平直线上)。已知AB=50m,DE=10m,求障碍物B,C两点间的距离。(结果精确到1m,参考数据: ![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学图书馆上周借书记录如下(以100册为标准,超过的册数记为正,不足的册数记为负):

(1)上星期五借出多少册?
(2)上星期四比上星期三多借出多少册?
(3)上周平均每天借出多少册?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列问题:
(1)计算:6÷(-![]() +
+![]() ).
).

方方同学的计算过程如下:原式=6÷(-![]() )+6÷
)+6÷![]() =-12+18=6.
=-12+18=6.
请你判断方方同学的计算过程是否正确,若不正确,请你写出正确的计算过程.
(2)请你参考黑板中老师的讲解,用运算律简便计算(请写出具体的解题过程):
①999×(-15);②999×![]() +333×(-
+333×(-![]() )-999×
)-999×![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问:在进行爆破时,公路AB段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
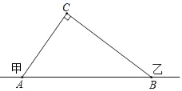
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com