
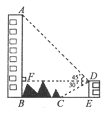
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为300,测得大楼顶端 A的仰角为450(点B,C,E在同一水平直线上)。已知AB=50m,DE=10m,求障碍物B,C两点间的距离。(结果精确到1m,参考数据: ![]() )
)

【答案】障碍物B,C两点间的距离约为23 m
【解析】试题分析:过点D作DF⊥AB于点F,过点C作CH⊥DF于点H,则DE=BF=CH=20m,根据直角三角形的性质得出DF的长,在Rt△CDE中,利用锐角三角函数的定义得出CE的长,根据BC=BE-CE即可得出结论.
试题解析:
过点D作DF⊥AB交于AB于点F,则∠DFA=900,∠ADA=450,∠FDC=300,
∵AB⊥BE于点B,DE⊥BE于点E,
∴∠BFD=∠FBE=∠BED=900.
∴四边形BEDF是矩形
∴BF=DE,FD=BE,FD∥BE.
∵AB=50,DE=10,
∴AF=AB-BF=40
在RtΔAFD中, ![]() ,
,
∴DF=AF=40
∵FD∥BE,∴∠DCE=∠FDC=300.
在RtΔCDE中![]() ,
,
∴![]()
∴![]()
答:障碍物B,C两点间的距离约为23m.


科目:初中数学 来源: 题型:
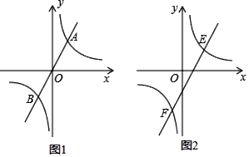
【题目】.如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线![]() 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.
(1)求直线y=kx+b(k≠0)的解析式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标(直接写出结果).
S△BOC,求点P的坐标(直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,在平行四边形 ABCD 中,对角线 AC 、 BD 交于点 O ,并且 DAC 60 ,ADB 15 ,点 E 是 AD 上一动点,延长 EO 交 BC 于点 F 。当点 E 从 D 点向 A 点移动 过程中(点 E 与点 D 、点 A 不重合),则四边形 AFCE 的变化是( )
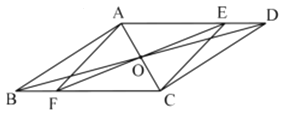
A.平行四边形→矩形→平行四边形→菱形→平行四边形
B.平行四边形→矩形→平行四边形→正方形→平行四边形
C.平行四边形→菱形→平行四边形→矩形→平行四边形
D.平行四边形→矩形→菱形→正方形→平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下表,回答问题:
x | … | -2 | -1 | 0 | 1 | 2 | … |
-2x+5 | … | 9 | 7 | 5 | 3 | a | … |
2x+8 | … | 4 | 6 | 8 | 10 | b | … |
(初步感知)
(1)a= ;b= ;
(归纳规律)
(2)随着x值的变化,两个代数式的值变化规律是什么?
(问题解决)
(3)比较-2x+5与2x+8的大小;
(4)请写出一个含x的代数式,要求x的值每增加1,代数式的值减小5,当x=0时,
代数式的值为-7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=mx(m为常数)与双曲线y=![]() (k为常数)相交于A、B两点.
(k为常数)相交于A、B两点.
(1)若点A的横坐标为3,点B的纵坐标为﹣4
①直接写出:k=____,m=____;
②点C在第一象限内是双曲线y=![]() 的点,当S△OAC=9时,求点C的坐标;
的点,当S△OAC=9时,求点C的坐标;
(2)将直线y=mx向右平移得到直线y=mx+b,交双曲线y=![]() 于点E(4,y1)和F(﹣2,y2),直接写出不等式mx2+bx<k的解集:_____.
于点E(4,y1)和F(﹣2,y2),直接写出不等式mx2+bx<k的解集:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1)在RtΔABC中,∠ACB=900,∠B=600,在图中作出∠ACB的三等分线CD,CE.(要求:尺规作图,保留痕迹,不定作法)
(2)由(1)知,我们可以用尺规作出直角的三等分线,但是仅仅使用尺规却不能把任意一个角分成三等分,为此,人们发明了许多等分角的机械器具,如图(2)是用三张硬纸片自制的一个最简单的三分角器,与半圆O相接的AB带的长度与半圆的半径相等:BD带的长度任意,它的一边与直线AC形成一个直角,且志半圆相切于点B,假设需要将∠KSM三等分,如图(3),首先将角的顶点S置于BD上,角的一边SK经过点A,另一边SM与半圆相切,连接SO,则SB,SO为∠KSM的三等分线,请你证明。

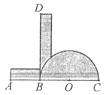

图(1) 图(2) 图(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】莹莹家里今年种植的猕猴桃获得大丰收,星期六从外地来了一位客商到村子里收购猕猴桃.莹莹家卖给了该客商10箱猕猴桃.莹莹在家里帮助爸爸记账,每标准箱猕猴桃的净重为5千克,超过标准数的部分记为“+”,不足标准数的部分记为“﹣”,莹莹的记录如下:+0.4、+0.6、﹣0.2、+0.1、﹣0.6、﹣0.3、+0.4、0、+0.7、﹣0.3.
(1)请计算这10箱猕猴桃的总重为多少千克?
(2)如果弥猴桃的价格为9元/千克,莹莹家出售这10箱猕猴桃共收入多少元?(精确到1元)
(3)若都用这种纸箱装,莹莹家的猕猴桃共能装约2000箱,按照目前这个价格,把猕猴桃全部出售,莹莹家大约能收入多少元?(精确到万位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列条件,能画出唯一△ABC的是( )
A.AB=4,BC=5,AC=1B.AB=5,BC=4,∠A=40°
C.∠A=60°,∠B=50°,AB=5D.∠C=90°,AB=8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
【答案】(1)2400元;(2)8台.
【解析】试题分析:(1)设商场第一次购入的空调每台进价是x元,根据题目条件“商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,每台的售价也上调了200元”列出分式方程解答即可;
(2)设最多将![]() 台空调打折出售,根据题目条件“在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售”列出不等式并解答即可.
台空调打折出售,根据题目条件“在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售”列出不等式并解答即可.
试题解析:(1)设第一次购入的空调每台进价是x元,依题意,得
![]() 解得
解得![]()
经检验, ![]() 是原方程的解.
是原方程的解.
答:第一次购入的空调每台进价是2 400元.
(2)由(1)知第一次购入空调的台数为24 000÷2 400=10(台),第二次购入空调的台数为10×2=20(台).
设第二次将y台空调打折出售,由题意,得
![]() 解得
解得![]()
答:最多可将8台空调打折出售.
【题型】解答题
【结束】
23
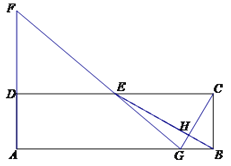
【题目】在矩形ABCD中,E为CD的中点,H为BE上的一点,,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证: AB·BH=2BG·EH
(2)若∠CGF=90°,![]() =3时,求
=3时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com