
【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
【答案】(1)2400元;(2)8台.
【解析】试题分析:(1)设商场第一次购入的空调每台进价是x元,根据题目条件“商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,每台的售价也上调了200元”列出分式方程解答即可;
(2)设最多将![]() 台空调打折出售,根据题目条件“在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售”列出不等式并解答即可.
台空调打折出售,根据题目条件“在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售”列出不等式并解答即可.
试题解析:(1)设第一次购入的空调每台进价是x元,依题意,得
![]() 解得
解得![]()
经检验, ![]() 是原方程的解.
是原方程的解.
答:第一次购入的空调每台进价是2 400元.
(2)由(1)知第一次购入空调的台数为24 000÷2 400=10(台),第二次购入空调的台数为10×2=20(台).
设第二次将y台空调打折出售,由题意,得
![]() 解得
解得![]()
答:最多可将8台空调打折出售.
【题型】解答题
【结束】
23
【题目】在矩形ABCD中,E为CD的中点,H为BE上的一点,,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证: AB·BH=2BG·EH
(2)若∠CGF=90°,![]() =3时,求
=3时,求![]() 的值.
的值.
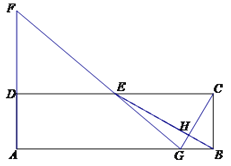
【答案】(1)见解析;(2)![]()
【解析】分析(1)根据相似三角形判定的方法,判断出△CEH∽△GBH,即可证明![]() .再由EC=
.再由EC=![]() CD=
CD=![]() AB可得结论;
AB可得结论;
(2)作EM⊥AB于M,则EM=BC=AD,AM=DE,设DE=CE=3a,则AB=CD=6a,由(1)得:![]() =3,得出BG=
=3,得出BG=![]() CE=a,AG=5a,证明△DEF∽△GEC,由相似三角形的性质得出EGEF=DEEC,由平行线证出
CE=a,AG=5a,证明△DEF∽△GEC,由相似三角形的性质得出EGEF=DEEC,由平行线证出![]() ,得出EF=
,得出EF= ![]() EG,求出EG=
EG,求出EG=![]() a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM=
a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM=![]() a,即可得出结果.
a,即可得出结果.
详解:(1)证明:∵四边形ABCD是矩形,
∴CD∥AB,
∴∠ECH=∠BGH,∠CEH=∠GBH,
∴△CEH∽△GBH,
∴![]() .
.
∴EC·BH=BG·EH
∴![]() AB·BH=BG·EH
AB·BH=BG·EH
∴AB·BH=2BG·EH
(2)作EM⊥AB于M,如图所示:
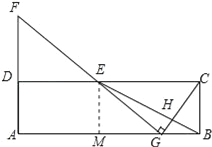
则EM=BC=AD,AM=DE,
∵E为CD的中点,
∴DE=CE,
设DE=CE=3a,则AB=CD=6a,
由(1)得:![]() =3,
=3,
∴BG=![]() CE=a,
CE=a,
∴AG=5a,
∵∠EDF=90°=∠CGF,∠DEF=∠GEC,
∴△DEF∽△GEC,
∴![]() ,
,
∴EGEF=DEEC,
∵CD∥AB,
∴![]() ,
,
∴![]() ,
,
∴EF=![]() EG,
EG,
∴EG![]() EG=3a3a,
EG=3a3a,
解得:EG=![]() a,
a,
在Rt△EMG中,GM=2a
∴EM=![]() a,
a,
∴BC=![]() a,
a,
∴![]() =
=![]()


科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为300,测得大楼顶端 A的仰角为450(点B,C,E在同一水平直线上)。已知AB=50m,DE=10m,求障碍物B,C两点间的距离。(结果精确到1m,参考数据: ![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点表示的数分别为-4,8.有一动点P从点A出发,第1次向左运动1个单位长度,第2次向右运动2个单位长度,第3次向左运动3个单位长度……按照此规律不断地运动.
(1)①当运动到第2020次时,点P表示的数是_______;
②点A与点B的距离AB=_______;
(2)点P会不会在某次运动时恰好到达某一个位置,使点P到点B的距离是点P到点A的距离的3倍?若存在,请求出此时点P表示的数;若不存在,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
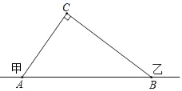
【题目】在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问:在进行爆破时,公路AB段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组乘一辆汽车沿公路东西方向检修线路,约定向东为正,某天从A地出发到收工时行走记录为(单位:千米):
+15、—2、+5、—1、—3、—2、+4、—5
(1)计算收工时,检修小组在A地的哪一边,距A地多远?
(2)若每千米汽车耗油量为0.4升,求出发到收工检修小组耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《道德经》中的“道生一,一生二,二生三,三生万物”道出了自然数的特征,在数的学习过程中,我们会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数,合数等,现在我们来研究另一种特珠的自然数“纯数”.
定义:对于自然数![]() ,在计算
,在计算![]() 时,各数位都不产生进位,则称这个自然数
时,各数位都不产生进位,则称这个自然数![]() 为“纯数”,例如:32是“纯数”,因为计算
为“纯数”,例如:32是“纯数”,因为计算![]() 时,各数位都不产生进位;23不是“纯数”,因为计算
时,各数位都不产生进位;23不是“纯数”,因为计算![]() 时,个位产生了进位.
时,个位产生了进位.
(1)判断2019和2020是否是“纯数”?请说明理由;
(2)求出不大于100的“纯数”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)解方程组:
① 
②![]()
(2)计算
①(π-2013)0-(![]() )-2+|-4|;
)-2+|-4|;
②4(a+2)(a+1)-7(a+3)(a-3)
(3)因式分解
①a4-16
②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AD=4,AB=3,如果点E在边BC上,将纸片沿AE折叠,使点B落在点F处,联结FC,当△EFC是直角三角形时,那么BE的长为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com