
【题目】《道德经》中的“道生一,一生二,二生三,三生万物”道出了自然数的特征,在数的学习过程中,我们会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数,合数等,现在我们来研究另一种特珠的自然数“纯数”.
定义:对于自然数![]() ,在计算
,在计算![]() 时,各数位都不产生进位,则称这个自然数
时,各数位都不产生进位,则称这个自然数![]() 为“纯数”,例如:32是“纯数”,因为计算
为“纯数”,例如:32是“纯数”,因为计算![]() 时,各数位都不产生进位;23不是“纯数”,因为计算
时,各数位都不产生进位;23不是“纯数”,因为计算![]() 时,个位产生了进位.
时,个位产生了进位.
(1)判断2019和2020是否是“纯数”?请说明理由;
(2)求出不大于100的“纯数”的个数.
【答案】(1)2019不是纯数,2020是纯数,理由见解析;(2)13
【解析】
(1)根据题目中的新定义可以解答本题,注意各数位都不产生进位的自然数才是“纯数”;
(2)根据题意可以推出不大于100的“纯数”的个数,本题得以解决.
解:(1)2019不是“纯数”,2020是“纯数”,
理由:当n=2019时,n+1=2020,n+2=2021,
∵个位是9+0+1=10,需要进位,
∴2019不是“纯数”;
当n=2020时,n+1=2021,n+2=2022,
∵个位是0+1+2=3,不需要进位,十位是2+2+2=6,不需要进位,百位为0+0+0=0,不需要进位,千位为2+2+2=6,不需要进位,
∴2020是“纯数”;
(2)由题意可得,
连续的三个自然数个位数字是0,1,2,其他位的数字为0,1,2,3时,不会
产生进位,
当这个数是一位自然数时,只能是0,1,2,共三个,
当这个自然数是两位自然数时,十位数字是1,2,3,个位数是0,1,2,共九个,
当这个数是三位自然数时,只能是100,
由上可得,不大于100的“纯数”的个数为3+9+1=13,
即不大于100的“纯数”的有13个.


科目:初中数学 来源: 题型:
【题目】莹莹家里今年种植的猕猴桃获得大丰收,星期六从外地来了一位客商到村子里收购猕猴桃.莹莹家卖给了该客商10箱猕猴桃.莹莹在家里帮助爸爸记账,每标准箱猕猴桃的净重为5千克,超过标准数的部分记为“+”,不足标准数的部分记为“﹣”,莹莹的记录如下:+0.4、+0.6、﹣0.2、+0.1、﹣0.6、﹣0.3、+0.4、0、+0.7、﹣0.3.
(1)请计算这10箱猕猴桃的总重为多少千克?
(2)如果弥猴桃的价格为9元/千克,莹莹家出售这10箱猕猴桃共收入多少元?(精确到1元)
(3)若都用这种纸箱装,莹莹家的猕猴桃共能装约2000箱,按照目前这个价格,把猕猴桃全部出售,莹莹家大约能收入多少元?(精确到万位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佳佳想探究一元三次方程x3+2x2-x-2=0的解的情况.根据以往的学习经验他想到了方程与函数的关系:一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一次方程kx+b=0(k≠0)的解;二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解.如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为方程x2-2x-3=0的解.
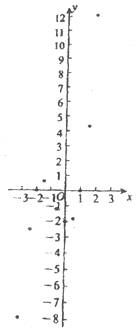
根据以上方程与函数的关系,若知道函数y=x3+2x2-x-2的图象与x轴交点的横坐标,即可知道方程x3+2x2-x-2=0的解.
佳佳为了解函数y=x3+2x2-x-2的图象,通过描点法画出函数的图象:

(1)直接写出m的值________,并画出函数图象;
(2)根据表格和图象可知,方程的解有________个,分别为________________;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
【答案】(1)2400元;(2)8台.
【解析】试题分析:(1)设商场第一次购入的空调每台进价是x元,根据题目条件“商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,每台的售价也上调了200元”列出分式方程解答即可;
(2)设最多将![]() 台空调打折出售,根据题目条件“在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售”列出不等式并解答即可.
台空调打折出售,根据题目条件“在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售”列出不等式并解答即可.
试题解析:(1)设第一次购入的空调每台进价是x元,依题意,得
![]() 解得
解得![]()
经检验, ![]() 是原方程的解.
是原方程的解.
答:第一次购入的空调每台进价是2 400元.
(2)由(1)知第一次购入空调的台数为24 000÷2 400=10(台),第二次购入空调的台数为10×2=20(台).
设第二次将y台空调打折出售,由题意,得
![]() 解得
解得![]()
答:最多可将8台空调打折出售.
【题型】解答题
【结束】
23
【题目】在矩形ABCD中,E为CD的中点,H为BE上的一点,,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证: AB·BH=2BG·EH
(2)若∠CGF=90°,![]() =3时,求
=3时,求![]() 的值.
的值.
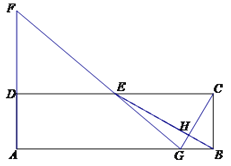
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有两点A、B,点A表示的数是4,点B表示的数是﹣11,点C是数轴上一动点.
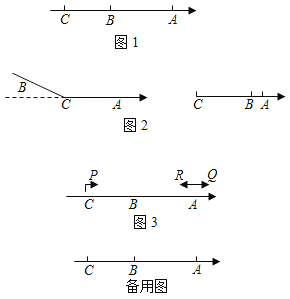
(1)如图1,若点C在点B的左侧,且BC:AB=3:5,求点C到原点的距离.
(2)如图2,若点C在A、B两点之间时,以点C为折点,将此数轴向右对折,当A、B两点之间的距离为1时,求C点在数轴上对应的数是多少?
(3)如图3,在(1)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度的2倍少5个单位长度/秒.经过4秒,点P、Q之间的距离是点Q、R之间距离的一半,求动点Q的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】防洪大堤的横截面如图所示,已知AE∥BC,背水坡AB的坡度![]() ,且AB=20米.身高1.7米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度为( )
,且AB=20米.身高1.7米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度为( )
(结果精确到整数,参考数据:sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)
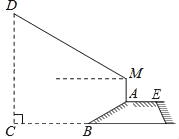
A. 30米 B. 32米 C. 34米 D. 36米
查看答案和解析>>
科目:初中数学 来源: 题型:
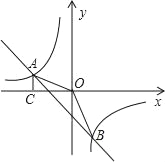
【题目】如图,一次函数y=kx﹣2的图象与反比例函数的图象交于A、B两点,过A作AC⊥x轴于点C.已知cos∠AOC=![]() ,OA=
,OA=![]() .
.
(1)求反比例函数及直线AB的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南岸区正全力争创全国卫生城区和全国文明城区(简称“两城同创”).某街道积极响应“两城同创”活动,投入一定资金绿化一块闲置空地,购买了甲、乙两种树木共72棵,甲种树木单价是乙种树木单价的![]() ,且乙种树木每棵80元,共用去资金6160元.
,且乙种树木每棵80元,共用去资金6160元.
(1)求甲、乙两种树木各购买了多少棵?
(2)经过一段时间后,种植的这批树木成活率高,绿化效果好.该街道决定再购买一批这两种树木绿化另一块闲置空地,两种树木的购买数量均与第一批相同,购买时发现甲种树木单价上涨了a%,乙种树木单价下降了![]() ,且总费用为6804元,求a的值.
,且总费用为6804元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,AB=AC,∠ABC =
中,AB=AC,∠ABC =![]() ,D是BC边上一点,以AD为边作
,D是BC边上一点,以AD为边作![]() ,使AE=AD,
,使AE=AD,![]() +
+![]() =180°.
=180°.
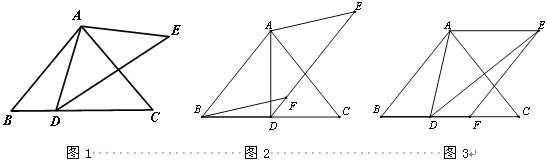
(1)直接写出∠ADE的度数(用含![]() 的式子表示);
的式子表示);
(2)以AB,AE为边作平行四边形ABFE,
①如图2,若点F恰好落在DE上,求证:BD=CD;
②如图3,若点F恰好落在BC上,求证:BD=CF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com