
【题目】佳佳想探究一元三次方程x3+2x2-x-2=0的解的情况.根据以往的学习经验他想到了方程与函数的关系:一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一次方程kx+b=0(k≠0)的解;二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解.如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为方程x2-2x-3=0的解.
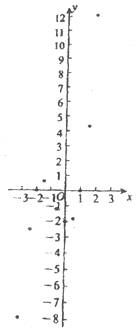
根据以上方程与函数的关系,若知道函数y=x3+2x2-x-2的图象与x轴交点的横坐标,即可知道方程x3+2x2-x-2=0的解.
佳佳为了解函数y=x3+2x2-x-2的图象,通过描点法画出函数的图象:

(1)直接写出m的值________,并画出函数图象;
(2)根据表格和图象可知,方程的解有________个,分别为________________;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集________________.
【答案】(1)m=0,图象见解析;(2)方程的解有三个,分别是-2,-1,1;(3)不等式的解集是-2<x<-1或x>1.
【解析】试题分析:(1)求出x=-1时的函数值即可解决问题;利用描点法画出图象即可;
(2)利用图象以及表格即可解决问题;
(3)不等式x3+2x2>x+2的解集,即为函数y=x3+2x2-x-2的函数值大于0的自变量的取值范围,观察图象即可解决问题;
试题解析:
(1)由题意m=-1+2+1-2=0.
函数图象如图所示.
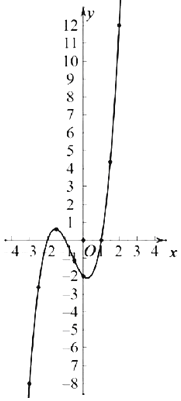
(2)根据表格和图象可知,方程的解有3个,分别为-2,或-1或1.
故答案为3,-2,或-1或1.
(3)不等式x3+2x2>x+2的解集,即为函数y=x3+2x2-x-2的函数值大于0的自变量的取值范围.
观察图象可知,-2<x<-1或x>1.


科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
(1)求证:四边形AMCN是平行四边形;
(2)若AC=BC=5,AB=6,求四边形AMCM的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列问题:
(1)计算:6÷(-![]() +
+![]() ).
).

方方同学的计算过程如下:原式=6÷(-![]() )+6÷
)+6÷![]() =-12+18=6.
=-12+18=6.
请你判断方方同学的计算过程是否正确,若不正确,请你写出正确的计算过程.
(2)请你参考黑板中老师的讲解,用运算律简便计算(请写出具体的解题过程):
①999×(-15);②999×![]() +333×(-
+333×(-![]() )-999×
)-999×![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点表示的数分别为-4,8.有一动点P从点A出发,第1次向左运动1个单位长度,第2次向右运动2个单位长度,第3次向左运动3个单位长度……按照此规律不断地运动.
(1)①当运动到第2020次时,点P表示的数是_______;
②点A与点B的距离AB=_______;
(2)点P会不会在某次运动时恰好到达某一个位置,使点P到点B的距离是点P到点A的距离的3倍?若存在,请求出此时点P表示的数;若不存在,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在网上销售苹果,原计划每天卖100斤,但实际每天的销量与计划销量相比有出入,如表是某周7天的销售情况(超额记为正,不足记为负.单位:斤):

(1)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 斤;
(2)本周实际销售总量达到了计划销量没有?
(3)若每斤按5元出售,每斤苹果的运费为1元,那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问:在进行爆破时,公路AB段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
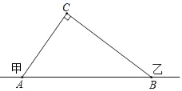
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《道德经》中的“道生一,一生二,二生三,三生万物”道出了自然数的特征,在数的学习过程中,我们会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数,合数等,现在我们来研究另一种特珠的自然数“纯数”.
定义:对于自然数![]() ,在计算
,在计算![]() 时,各数位都不产生进位,则称这个自然数
时,各数位都不产生进位,则称这个自然数![]() 为“纯数”,例如:32是“纯数”,因为计算
为“纯数”,例如:32是“纯数”,因为计算![]() 时,各数位都不产生进位;23不是“纯数”,因为计算
时,各数位都不产生进位;23不是“纯数”,因为计算![]() 时,个位产生了进位.
时,个位产生了进位.
(1)判断2019和2020是否是“纯数”?请说明理由;
(2)求出不大于100的“纯数”的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com