
【题目】某检修小组乘一辆汽车沿公路东西方向检修线路,约定向东为正,某天从A地出发到收工时行走记录为(单位:千米):
+15、—2、+5、—1、—3、—2、+4、—5
(1)计算收工时,检修小组在A地的哪一边,距A地多远?
(2)若每千米汽车耗油量为0.4升,求出发到收工检修小组耗油多少升?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,将点
中,将点![]() 翻折到对角线
翻折到对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 交
交![]() 于点
于点![]() .将点
.将点![]() 翻折到对角线
翻折到对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 交
交![]() 于点
于点![]() .
.
![]() 求证:四边形
求证:四边形![]() 为平行四边形;
为平行四边形;
![]() 若四边形
若四边形![]() 为菱形,且
为菱形,且![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):

①接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
②若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
③若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形,在图1正方形网格(每个小正方形边长为1)中画出格点△ABC,使AB=AC=5,BC=![]()
(2)在△ABC中, AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图2所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图2所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
①△ABC的面积为: .
②若△DEF三边的长分别为![]() 、
、![]() 、
、![]() ,请在图3的正方形网格中画出相应的△DEF,并利用构图法求出它的面积为_____________.
,请在图3的正方形网格中画出相应的△DEF,并利用构图法求出它的面积为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=mx2-6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
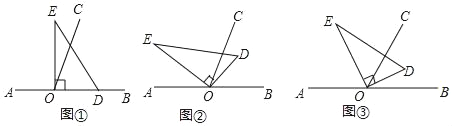
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OC恰好平分∠BOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com