
【题目】根据下列条件,能画出唯一△ABC的是( )
A.AB=4,BC=5,AC=1B.AB=5,BC=4,∠A=40°
C.∠A=60°,∠B=50°,AB=5D.∠C=90°,AB=8
【答案】C
【解析】
要满足唯一画出△ABC,就要求选项给出的条件符合三角形全等的判定方法,不符合判定方法的画出的图形不一样,也就是三角形不唯一,而各选项中只有C选项符合ASA,是满足题目要求的,于是答案可得
A、因为AB+ AC= BC,所以这三边不能构成三角形,故本选项不符合题意;
B、根据AB=5,BC=4,∠A=40°不能画出唯一三角形,如图所示△ABD和△ABC,故本选项不符合题意;
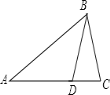
C、根据∠A=60°,∠B=50°,AB=5,符合全等三角形的判定定理ASA,即能画出唯一三角形,故本选项正确;
D、只有一个角和一个边无法根据此作出一个唯一的三角形,故本选项不符合题意;
故选:C
根据题意得,


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)|﹣3|﹣5×(﹣![]() )+(﹣4)
)+(﹣4)
(2)(﹣2)2﹣4÷(﹣![]() )+(﹣1)2016
)+(﹣1)2016
(3)![]() ×(﹣24)
×(﹣24)
(4)﹣12014﹣(1﹣0.5)÷![]() ×[(﹣2)3﹣4]
×[(﹣2)3﹣4]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为300,测得大楼顶端 A的仰角为450(点B,C,E在同一水平直线上)。已知AB=50m,DE=10m,求障碍物B,C两点间的距离。(结果精确到1m,参考数据: ![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量![]() (升)与行驶路程
(升)与行驶路程![]() (千米)之间是一次函数关系,其部分图象如图所示.
(千米)之间是一次函数关系,其部分图象如图所示.
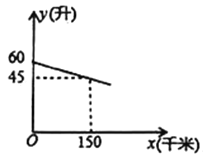
(1)求![]() 关于
关于![]() 的函数关系式;(不需要写自变量
的函数关系式;(不需要写自变量![]() 的取值范围)
的取值范围)
(2)已知当油箱中的剩余油量为10升时,该汽车会开始提示加油,在此次行驶过程中,行驶了482千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列问题:
(1)计算:6÷(-![]() +
+![]() ).
).

方方同学的计算过程如下:原式=6÷(-![]() )+6÷
)+6÷![]() =-12+18=6.
=-12+18=6.
请你判断方方同学的计算过程是否正确,若不正确,请你写出正确的计算过程.
(2)请你参考黑板中老师的讲解,用运算律简便计算(请写出具体的解题过程):
①999×(-15);②999×![]() +333×(-
+333×(-![]() )-999×
)-999×![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点P是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C,D.
(1)∠PCD=∠PDC吗?为什么?
(2)OP是CD的垂直平分线吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点表示的数分别为-4,8.有一动点P从点A出发,第1次向左运动1个单位长度,第2次向右运动2个单位长度,第3次向左运动3个单位长度……按照此规律不断地运动.
(1)①当运动到第2020次时,点P表示的数是_______;
②点A与点B的距离AB=_______;
(2)点P会不会在某次运动时恰好到达某一个位置,使点P到点B的距离是点P到点A的距离的3倍?若存在,请求出此时点P表示的数;若不存在,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)解方程组:
① 
②![]()
(2)计算
①(π-2013)0-(![]() )-2+|-4|;
)-2+|-4|;
②4(a+2)(a+1)-7(a+3)(a-3)
(3)因式分解
①a4-16
②![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com