
����Ŀ��һ�������������������ֲ�������̽�����������������Ĺ��̣�������һ��������������һ��.
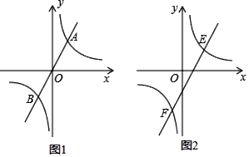
�����ֲ��룩��1����ͼ�٣���֪��AOB��70������AOD��100����OCΪ��BOD�Ľ�ƽ���ߣ����AOC�Ķ���Ϊ ��.


��̽�����ɣ���2����ͼ�٣���AOB��m����AOD��n��OCΪ��BOD�Ľ�ƽ����. �����AOC�Ķ������ú�m��n�Ĵ���ʽ��ʾ������˵������.
������������3����ͼ�ڣ�����AOB��20������AOC��90������AOD��120��.������OB�Ƶ�O��ÿ��20����ʱ����ת������OC�Ƶ�O��ÿ��10��˳ʱ����ת������OD�Ƶ�Oÿ��30��˳ʱ����ת����������ͬʱ��ת����һ��������ֱ��OA�غ�ʱ����������ͬʱֹͣ�˶�. �˶�����ʱ������һ�������������������нǵĽ�ƽ���ߣ�
���𰸡���1��85������2����AOC��![]() �����ɼ���������3������
�����ɼ���������3������![]() ��
��![]() ��4��ʱ������һ�������������������нǵ�ƽ����.
��4��ʱ������һ�������������������нǵ�ƽ����.
��������
��1�����ݡ�AOD����AOB����BOD֮��Ĺ�ϵ�������BOD�Ķ�����Ȼ����ݽ�ƽ���ߵ����������BOC�Ķ������ټ����AOC���ɽ������.
��2�����ݡ�AOD����AOB����BOD֮��Ĺ�ϵ����m��n��ʾ����BOD�Ķ�����Ȼ����ݽ�ƽ���ߵ�������m��n�Ĵ���ʽ��ʾ����BOC������ٱ�ʾ����AOC���ɽ������.
��3�����ݸ���֮����ڵ�������ϵ���辭��x��ʱ���ֱ���x����DOA����COA����BOA��ʾ������Ȼ�������������ۣ����ݽ�ƽ���ߵ������г����̣��������.
��1��85����
��2���ߡ�AOB��m����AOD��n
���BOD��n��m
��OCΪ��BOD�Ľ�ƽ����
���BOC��![]()
���AOC��![]() +m��
+m��![]()
��3���辭����ʱ��Ϊx�룬
���DOA��120����30x����COA��90����10x����BOA��20��+20x��
�ٵ���x��![]() ֮ǰ��OCΪOB��OD�Ľ�ƽ���ߣ�30��20x��70��30x��x1��4���ᣩ��
֮ǰ��OCΪOB��OD�Ľ�ƽ���ߣ�30��20x��70��30x��x1��4���ᣩ��
�ڵ�x��![]() ��2֮�䣬ODΪOC��OB�Ľ�ƽ���ߣ���30+20x��100��50x��x2��
��2֮�䣬ODΪOC��OB�Ľ�ƽ���ߣ���30+20x��100��50x��x2��![]() ��
��
�۵�x��2��![]() ֮�䣬OBΪOC��OD�Ľ�ƽ���ߣ�70��30x����100+50x��x3��
֮�䣬OBΪOC��OD�Ľ�ƽ���ߣ�70��30x����100+50x��x3��![]() ��
��
�ܵ�x��![]() ��4֮�䣬OCΪOB��OD�Ľ�ƽ���ߣ���70+30x����30+20x��x4��4.
��4֮�䣬OCΪOB��OD�Ľ�ƽ���ߣ���70+30x����30+20x��x4��4.
�𣺾���![]() ��
��![]() ��4��ʱ������һ�������������������нǵ�ƽ����.
��4��ʱ������һ�������������������нǵ�ƽ����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������˾����114�ֻ���ƻ�ͬʱ���A��B�����ͺŵij�������������һ���˻������ϵ�һ����Ϣ�ǣ�
A�ͳ������أ� | B�ͳ������أ� | �˻����� |
3�� | 2�� | 38�� |
1�� | 3�� | 36�� |
����������Ϣ�������������⣺
��1��1��A�ͳ���1��B�ͳ���װ������һ�οɷֱ��˻����ٶ֣�
��2����������˾����һ�����꣬��ǡ��ÿ������װ�����������������˾����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı��� ABCD ���������ĸ��������� AB �� CD ���� BC �� AD ���� AB CD ����ABC ADC �������ĸ���������ѡ��������ʹ�ı��� ABCD ��Ϊƽ���ı��ε�ѡ���У� ��
A.3 ��B.4 ��C.5 ��D.6 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����������ڽǵĶ���֮����180�㣬��ͼ���������ǰ岻ͬλ�õİڷţ����С�ACB=��CDE=90�㣬��BAC=60�㣬��DEC=45��.
��1����AB��CDʱ����ͼ�٣����DCB�Ķ�����
��2����CD��CB�غ�ʱ����ͼ�ڣ��ж�DE��AC��λ�ù�ϵ��˵�����ɣ�
��3����ͼ�ۣ�����DCB= ʱ��AB��CE.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������С�����εı߳���Ϊ1����λ��A��B��C���ڸ���ϣ�

��1������C���߶�AB��ƽ����CD��
��2������A���߶�BC�Ĵ��ߣ�����ΪE��
��3���߶�AE�ij����ǵ� ��ֱ�� �ľ��룻
��4���Ƚ��߶�AE��AB��BC�Ĵ�С��ϵ�������������ӣ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y��mx(mΪ����)��˫����y��![]() (kΪ����)�ཻ��A��B���㣮
(kΪ����)�ཻ��A��B���㣮
(1)����A�ĺ�����Ϊ3����B��������Ϊ��4
��ֱ��д����k��____��m��____��
�ڵ�C�ڵ�һ��������˫����y��![]() �ĵ㣬��S��OAC��9ʱ�����C�����ꣻ
�ĵ㣬��S��OAC��9ʱ�����C�����ꣻ
(2)��ֱ��y��mx����ƽ�Ƶõ�ֱ��y��mx+b����˫����y��![]() �ڵ�E(4��y1)��F(��2��y2)��ֱ��д������ʽmx2+bx��k�Ľ⼯��_____��
�ڵ�E(4��y1)��F(��2��y2)��ֱ��д������ʽmx2+bx��k�Ľ⼯��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ABΪ��O��ֱ����BD��CDΪ��O�����ߣ��е�ֱ�ΪB��C��
��1����֤��AC��OD��
��2����BC=BD����BD=6cmʱ����ͼ����Ӱ���ֵ�����������ȡ����ֵ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����б���֮���ϵ�У�һ����������һ����������������������( )
A.�����ε����S���ű߳�x�ı仯���仯
B.�����ε��ܳ�C���ű߳�x�ı仯���仯
C.ˮ����ˮ10������0.5��/�ֵ����������ˮ��ʣˮ��(��)���ŷ�ˮʱ��t(��)�ı仯���仯
D.���Ϊ20�������ε�һ��a��������ϵĸ�h�ı仯���仯
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E��F�ֱ���������ABCD��AD��BC�ϵ������㣬M���߶�EF�ϵ�һ�㣬��M��ֱ����������ABCD�ı߽��ڵ�P�͵�H����PH=EF��������������ֱ��PH�����( )��
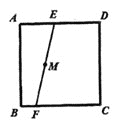
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com