
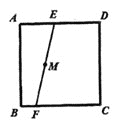
【题目】如图,E,F分别是正方形ABCD边AD、BC上的两定点,M是线段EF上的一点,过M的直线与正方形ABCD的边交于点P和点H,且PH=EF,则满足条件的直线PH最多有( )条
A.1B.2C.3D.4
【答案】C
【解析】
如图1,过点B作BG∥EF,过点C作CN∥PH,利用正方形的性质,可证得AB∥CD,AD∥BC,∠A=∠NBC=90°,AB=BC,再证明BG=CN,利用HL证明Rt△ABG≌Rt△CBN,根据全等三角形的对应角相等,可知∠ABG=∠BCN,然后证明PH⊥EF即可,因此过点M作EF的垂线满足的有一条直线;图2中还有2条,即可得出答案.
解:如图1,过点B作BG∥EF,过点C作CN∥PH,
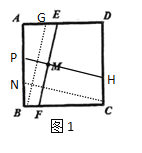
∵正方形ABCD,
∴AB∥CD,AD∥BC,∠A=∠NBC=90°,AB=BC,
∴四边形BGEF,四边形PNCH是平行四边形,
EF=BG,PH=CN,
∵PH=EF,
∴BG=CN,
在Rt△ABG和Rt△CBN中,
![]()
∴Rt△ABG≌Rt△CBN(HL)
∴∠ABG=∠BCN,
∵∠ABG+∠GBC=90°
∴∠BCN+∠GBC=90°,
∴BG⊥CN,
∴PH⊥EF,
∴过点M作EF的垂线满足的有一条直线;
如图2

图2中有两条P1H1,P2H2,
所以满足条件的直线PH最多有3条,
故答案为:C


科目:初中数学 来源: 题型:
【题目】一个问题解决往往经历发现猜想——探索归纳——问题解决的过程,下面结合一道几何题来体验一下.
(发现猜想)(1)如图①,已知∠AOB=70°,∠AOD=100°,OC为∠BOD的角平分线,则∠AOC的度数为 ;.


(探索归纳)(2)如图①,∠AOB=m,∠AOD=n,OC为∠BOD的角平分线. 猜想∠AOC的度数(用含m、n的代数式表示),并说明理由.
(问题解决)(3)如图②,若∠AOB=20°,∠AOC=90°,∠AOD=120°.若射线OB绕点O以每秒20°逆时针旋转,射线OC绕点O以每秒10°顺时针旋转,射线OD绕点O每秒30°顺时针旋转,三条射线同时旋转,当一条射线与直线OA重合时,三条射线同时停止运动. 运动几秒时,其中一条射线是另外两条射线夹角的角平分线?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在Rt△ABC中,∠A=90°,AB=AC=4.点E为Rt△ABC边上一点,以每秒1单位的速度从点C出发,沿着C→A→B的路径运动到点B为止.连接CE,以点C为圆心,CE长为半径作⊙C,⊙C与线段BC交于点D.设扇形DCE面积为S,点E的运动时间为t.则在以下四个函数图象中,最符合扇形面积S关于运动时间t的变化趋势的是( )

A. 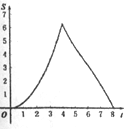 B.
B. 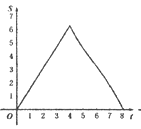
C. 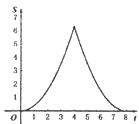 D.
D. 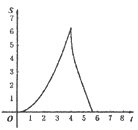
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在网上销售苹果,原计划每天卖100斤,但实际每天的销量与计划销量相比有出入,如表是某周7天的销售情况(超额记为正,不足记为负.单位:斤):

(1)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 斤;
(2)本周实际销售总量达到了计划销量没有?
(3)若每斤按5元出售,每斤苹果的运费为1元,那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都是1,正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积为( )

A. ![]() B.
B. ![]() C. 3 D. 5
C. 3 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问:在进行爆破时,公路AB段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
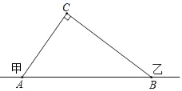
查看答案和解析>>
科目:初中数学 来源: 题型:
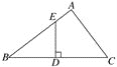
【题目】已知,如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2-EA2=AC2,
(1)求证:∠A=90°.
(2)若DE=3,BD=4,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蛋糕店为了吸引顾客,在A、B两种蛋糕中,轮流降低其中一种蛋糕价格,这样形成两种盈利模式,模式一:A种蛋糕利润每盒8元,B种蛋糕利润每盒15元;模式二:A种蛋糕利润每盒14元,B种蛋糕利润每盒11元每天限定销售A、B两种蛋糕共40盒,且都能售完,设每天销售A种蛋糕x盒
(1)设按模式一销售A、B两种蛋糕所获利润为y1元,按模式二销售A、B两种蛋糕所获利润为y2元,分别求出y1、y2关于x的函数解析式;
(2)在同一个坐标系内分别画出(1)题中的两个函数的图象;

(3)若y始终表示y1、y2中较大的值,请问y是否为x的函数,并说说你的理由,并直接写出y的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com