
ΓΨΧβΡΩΓΩΡ≥ΒΑΗβΒξΈΣΝΥΈϋ“ΐΙΥΩΆΘ§‘ΎAΓΔBΝΫ÷÷ΒΑΗβ÷–Θ§¬÷ΝςΫΒΒΆΤδ÷–“Μ÷÷ΒΑΗβΦέΗώΘ§’β―υ–Έ≥…ΝΫ÷÷”·άϊΡΘ ΫΘ§ΡΘ Ϋ“ΜΘΚA÷÷ΒΑΗβάϊ»σΟΩΚ–8‘ΣΘ§B÷÷ΒΑΗβάϊ»σΟΩΚ–15‘ΣΘΜΡΘ ΫΕΰΘΚA÷÷ΒΑΗβάϊ»σΟΩΚ–14‘ΣΘ§B÷÷ΒΑΗβάϊ»σΟΩΚ–11‘ΣΟΩΧλœόΕ®œζ έAΓΔBΝΫ÷÷ΒΑΗβΙ≤40Κ–Θ§«“ΕΦΡή έΆξΘ§…ηΟΩΧλœζ έA÷÷ΒΑΗβxΚ–
Θ®1Θ©…ηΑ¥ΡΘ Ϋ“Μœζ έAΓΔBΝΫ÷÷ΒΑΗβΥυΜώάϊ»σΈΣy1‘ΣΘ§Α¥ΡΘ ΫΕΰœζ έAΓΔBΝΫ÷÷ΒΑΗβΥυΜώάϊ»σΈΣy2‘ΣΘ§Ζ÷±π«σ≥ωy1ΓΔy2ΙΊ”ΎxΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©‘ΎΆ§“ΜΗωΉχ±ξœΒΡΎΖ÷±πΜ≠≥ω(1)Χβ÷–ΒΡΝΫΗωΚ· ΐΒΡΆΦœσΘΜ

Θ®3Θ©»τy Φ÷’±μ Ψy1ΓΔy2÷–Ϋœ¥σΒΡ÷ΒΘ§«κΈ y «ΖώΈΣxΒΡΚ· ΐΘ§≤ΔΥΒΥΒΡψΒΡάμ”…Θ§≤Δ÷±Ϋ”–¥≥ωyΒΡΉν–Γ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©y1==-7x+600Θ§y2==3x+440 Θ®2Θ©¥πΑΗΦϊΫβΈω Θ®3Θ©¥πΑΗΦϊΫβΈω
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΝΫ÷÷”·άϊΡΘ ΫΘ§Ζ÷±πΝ–≥ωy1ΓΔy2ΙΊ”ΎxΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©άϊ”ΟΟηΒψΖ®Μ≠≥ωΝΫΚ· ΐΆΦœώΘΜ
Θ®3Θ©”…y1=y2Θ§Ϋ®ΝΔΙΊ”ΎxΒΡΖΫ≥ΧΘ§ΫβΖΫ≥Χ«σ≥ωxΒΡ÷ΒΘ§ΨΆΩ…ΒΟΒΫΝΫΚ· ΐΒΡΫΜΒψΉχ±ξΘ§‘Όάϊ”Ο“Μ¥ΈΚ· ΐΒΡ–‘÷ Θ§ΨΆΩ…ΒΟ≥ωΒ±0ΓήxΓή40 ±Θ§y1ΥφxΒΡ‘ω¥σΕχ‘ω¥σΘ§y2ΥφxΒΡ‘ω¥σΕχΦθ–ΓΘ§Ω…ΒΟΒΫΟΩ“ΜΗωΉ‘±δΝΩxΕΦ”–Έ®“ΜΒΡ“ΜΗωyΒΡ÷Β”κ÷°Ε‘”ΠΘ§”…¥ΥΩ…ΒΟ≥ω≈–Εœ.
Θ®1Θ©ΫβΘΚ ”…Χβ“βΒΟΘΚ
y1=8x+15Θ®40-xΘ©=-7x+600Θ§
y2=14x+11Θ®40-xΘ©=3x+440 ΘΜ
Θ®2Θ©ΫβΘΚ »γΆΦΘ§
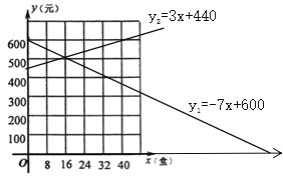
Θ®3Θ©ΫβΘΚ Β±y1=y2 ±Θ§-7x+600=3x+440
Ϋβ÷°ΘΚx=16
Γύx=16 ±Θ§y=3ΓΝ16+440=488
Β±0ΓήxΓή40 ±Θ§y1ΥφxΒΡ‘ω¥σΕχ‘ω¥σΘ§y2ΥφxΒΡ‘ω¥σΕχΦθ–ΓΘ§
Γύ![]()
ΓύΟΩ“ΜΗωΉ‘±δΝΩxΕΦ”–Έ®“ΜΒΡ“ΜΗωyΒΡ÷Β”κ÷°Ε‘”ΠΘ§
Γύy «xΒΡΚ· ΐΘ§Β±x=16 ±Θ§yΒΡΉν–Γ÷ΒΈΣ488.


 ΩΈΧΟ–ΓΉς“ΒœΒΝ–¥πΑΗ
ΩΈΧΟ–ΓΉς“ΒœΒΝ–¥πΑΗ ΜΤΗ‘–ΓΉ¥‘ΣΩΎΥψΥΌΥψΝΖœΑ≤αœΒΝ–¥πΑΗ
ΜΤΗ‘–ΓΉ¥‘ΣΩΎΥψΥΌΥψΝΖœΑ≤αœΒΝ–¥πΑΗ ≥…ΙΠ―ΒΝΖΦΤΜ°œΒΝ–¥πΑΗ
≥…ΙΠ―ΒΝΖΦΤΜ°œΒΝ–¥πΑΗ ±ΕΥΌ―ΒΝΖΖ®÷±Ά®÷–ΩΦΩΦΒψœΒΝ–¥πΑΗ
±ΕΥΌ―ΒΝΖΖ®÷±Ά®÷–ΩΦΩΦΒψœΒΝ–¥πΑΗ “ΜΨμΗψΕ®œΒΝ–¥πΑΗ
“ΜΨμΗψΕ®œΒΝ–¥πΑΗ Οϊ–ΘΉς“Β±ΨœΒΝ–¥πΑΗ
Οϊ–ΘΉς“Β±ΨœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–±δΝΩ÷°ΦδΙΊœΒ÷–Θ§“ΜΗω±δΝΩ «Νμ“ΜΗω±δΝΩΒΡ’ΐ±»άΐΚ· ΐΒΡ «( )
A.’ΐΖΫ–ΈΒΡΟφΜΐSΥφΉ≈±Ώ≥ΛxΒΡ±δΜ·Εχ±δΜ·
B.’ΐΖΫ–ΈΒΡ÷ή≥ΛCΥφΉ≈±Ώ≥ΛxΒΡ±δΜ·Εχ±δΜ·
C.Υ°œδ”–Υ°10…ΐΘ§“‘0.5…ΐ/Ζ÷ΒΡΝςΝΩΆυΆβΖ≈Υ°Θ§ ΘΥ°ΝΩ(…ΐ)ΥφΉ≈Ζ≈Υ° ±Έ t(Ζ÷)ΒΡ±δΜ·Εχ±δΜ·
D.ΟφΜΐΈΣ20ΒΡ»ΐΫ«–ΈΒΡ“Μ±ΏaΥφΉ≈’β±Ώ…œΒΡΗΏhΒΡ±δΜ·Εχ±δΜ·
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§EΘ§FΖ÷±π «’ΐΖΫ–ΈABCD±ΏADΓΔBC…œΒΡΝΫΕ®ΒψΘ§M «œΏΕΈEF…œΒΡ“ΜΒψΘ§ΙΐMΒΡ÷±œΏ”κ’ΐΖΫ–ΈABCDΒΡ±ΏΫΜ”ΎΒψPΚΆΒψHΘ§«“PH=EFΘ§‘ρ¬ζΉψΧθΦΰΒΡ÷±œΏPHΉνΕύ”–( )Χθ
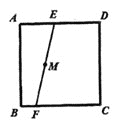
A.1B.2C.3D.4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ ΐ÷α…œ”–ΝΫΒψAΓΔBΘ§ΒψA±μ ΨΒΡ ΐ «4Θ§ΒψB±μ ΨΒΡ ΐ «©¹11Θ§ΒψC « ΐ÷α…œ“ΜΕ·ΒψΘ°
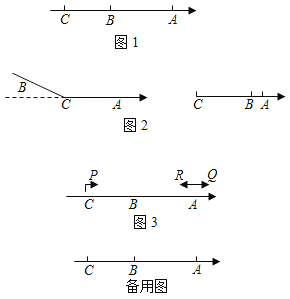
Θ®1Θ©»γΆΦ1Θ§»τΒψC‘ΎΒψBΒΡΉσ≤ύΘ§«“BCΘΚABΘΫ3ΘΚ5Θ§«σΒψCΒΫ‘≠ΒψΒΡΨύάκΘ°
Θ®2Θ©»γΆΦ2Θ§»τΒψC‘ΎAΓΔBΝΫΒψ÷°Φδ ±Θ§“‘ΒψCΈΣ’έΒψΘ§ΫΪ¥Υ ΐ÷αœρ”“Ε‘’έΘ§Β±AΓΔBΝΫΒψ÷°ΦδΒΡΨύάκΈΣ1 ±Θ§«σCΒψ‘Ύ ΐ÷α…œΕ‘”ΠΒΡ ΐ «Εύ…ΌΘΩ
Θ®3Θ©»γΆΦ3Θ§‘ΎΘ®1Θ©ΒΡΧθΦΰœ¬Θ§Ε·ΒψPΓΔQΝΫΒψΆ§ ±¥”CΓΔA≥ωΖΔœρ”“‘ΥΕ·Θ§Ά§ ±Ε·ΒψR¥”ΒψAœρΉσ‘ΥΕ·Θ§“―÷ΣΒψPΒΡΥΌΕ» «ΒψRΒΡΥΌΕ»ΒΡ3±ΕΘ§ΒψQΒΡΥΌΕ» «ΒψRΒΡΥΌΕ»ΒΡ2±Ε…Ό5ΗωΒΞΈΜ≥ΛΕ»/ΟκΘ°Ψ≠Ιΐ4ΟκΘ§ΒψPΓΔQ÷°ΦδΒΡΨύάκ «ΒψQΓΔR÷°ΦδΨύάκΒΡ“ΜΑκΘ§«σΕ·ΒψQΒΡΥΌΕ»Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–ΆΦ–Έ÷–Θ§ «÷αΕ‘≥ΤΆΦ–ΈΒΡ «Θ®ΓΓΓΓΘ©
A. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/3/27/1911053122682880/1914886922772480/STEM/c8503fddf66f4b8c93035a98d8f9f214.png] B.  C.
C.  D.
D. 
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
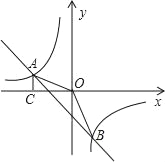
ΓΨΧβΡΩΓΩ»γΆΦΘ§“Μ¥ΈΚ· ΐy=kx©¹2ΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐΒΡΆΦœσΫΜ”ΎAΓΔBΝΫΒψΘ§ΙΐAΉςACΓΆx÷α”ΎΒψCΘ°“―÷ΣcosΓœAOC=![]() Θ§OA=
Θ§OA=![]() Θ°
Θ°
Θ®1Θ©«σΖ¥±»άΐΚ· ΐΦΑ÷±œΏABΒΡΫβΈω ΫΘΜ
Θ®2Θ©«σΓςAOBΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§EΒψΈΣDF…œΒΡΒψΘ§BΈΣAC…œΒΡΒψΘ§Γœ1=Γœ2Θ§ΓœC=ΓœDΘ°

‘ΥΒΟςΘΚACΓΈDFΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“ΜΗω≥ΛΖΫΧε≥Λ![]() Θ§Ωμ
Θ§Ωμ![]() Θ§ΗΏ
Θ§ΗΏ![]() .¥”’βΗω≥ΛΖΫΧεΒΡ“ΜΗωΫ«…œΆΎΒτ“ΜΗωάβ≥Λ
.¥”’βΗω≥ΛΖΫΧεΒΡ“ΜΗωΫ«…œΆΎΒτ“ΜΗωάβ≥Λ![]() ΒΡ’ΐΖΫΧεΘ§ Θœ¬≤ΩΖ÷ΒΡΧεΜΐ «Θ®______Θ©
ΒΡ’ΐΖΫΧεΘ§ Θœ¬≤ΩΖ÷ΒΡΧεΜΐ «Θ®______Θ©![]() Θ§ Θœ¬≤ΩΖ÷ΒΡ±μΟφΜΐ «Θ®______Θ©
Θ§ Θœ¬≤ΩΖ÷ΒΡ±μΟφΜΐ «Θ®______Θ©![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ ΐ–ΈΫαΚœ «÷Ί“ΣΒΡ ΐ―ßΥΦœκΖΫΖ®÷°“ΜΘ§ ΐ–ΈΫαΚœΨΏΧεΒΊΥΒΨΆ «ΫΪ≥ιœσ ΐ―ß”ο―‘”κ÷±ΙέΆΦ–ΈΫαΚœΤπά¥Θ§ Ι≥ιœσΥΦΈ§”κ–ΈœσΥΦΈ§ΫαΚœΤπά¥Θ§Ά®ΙΐΓΑ ΐΓ±”κΓΑ–ΈΓ±÷°ΦδΒΡΕ‘”ΠΚΆΉΣ±δά¥ΫβΨω ΐ―ßΈ ΧβΓΘ ΐ÷α « ΐ–ΈΫαΚœΒΡΉνΜυ¥ΓΆΦ–ΈΘ§ «Ν§Ϋ” ΐ”κ–ΈΒΡ«≈ΝΚ÷°“ΜΘ§«κΫβΨωœ¬ΟφΒΡΈ ΧβΘΚ
Θ®1Θ©»γΆΦ1Θ§ΒψB±μ ΨΒΡ ΐ «1Θ§‘ρΒψA±μ ΨΒΡ ΐ « .

Θ®2Θ©»γΙϊΒψM±μ Ψ ΐΘ≠2Θ§ΫΪΒψMœρ”““ΤΕ·6ΗωΒΞΈΜ≥ΛΕ»ΒΫ¥ο÷’ΒψNΘ§Ρ«Ο¥÷’ΒψN±μ ΨΒΡ ΐ «4Θ§¥Υ ±MΓΔNΝΫΒψΦδΒΡΨύάκ « .
Θ®3Θ©»τ®OxΘ≠0®O“β“ε±μ Ψ ΐxΒΫ‘≠ΒψΒΡΨύάκΘ§‘ρ®OxΘ≠3®OΒΡ“β“ε±μ Ψ ΐxΒΫ3ΒΡΨύάκΘΜάύΥΤΒΡ ΫΉ”®OxΘΪ3®O=4Θ§‘ρx= .
Θ®4Θ©”…Θ®3Θ©Ω…÷ΣΘ§“ΜΑψΒΊΘ§»γΙϊΒψA±μ Ψ ΐΈΣaΘ§ΒψB±μ ΨΒΡ ΐbΘ§‘ρAΓΔBΝΫΒψΦδΒΡΨύάκ±μ ΨΈΣ .
Θ®5Θ©»γΆΦ2Θ§ ΐ÷α…œΒΡΝΫΗωΒψAΓΔBΥυ±μ ΨΒΡ ΐΖ÷±π «aΘ§bΘ§ΒψOΈΣ‘≠ΒψΓΘ‘ΎaΘΪbΘ§aΘ≠bΘ§®Oa®OΘ≠®Ob®O’β»ΐΗω‘ΥΥψΫαΙϊ÷–Θ§ «’ΐ ΐΒΡ”– Ηω.
![]()
Θ®6Θ©άϊ”Ο ΐ÷α÷±Ϋ”–¥≥ω®OxΘ≠2®OΘΪ®OxΘΪ5®OΒΡΉν–Γ÷Β= .
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com