练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若实数m，n，p满足m＜n＜p（mp＜0）且|p|＜|n|＜|m|，则|x﹣m|+|x+n|+|x+p|的最小值是_____．

    【答案】﹣m﹣n．

    【解析】

    先根据mp＜0，确认p＞0，m＜0，再根据已知可得：n＜0，并画数轴标三个实数的位置及﹣n和﹣p的位置，根据图形可知：当x＝﹣p时，|x﹣m|+|x+n|+|x+p|有最小值，代入可得最小值．

    解：∵mp＜0，

    ∴m、p异号，

    ∵m＜p，

    ∴p＞0，m＜0，

    ∵m＜n＜p且|p|＜|n|＜|m|，

    ∴n＜0，

    如图所示：

    ∴当x＝﹣p时，|x﹣m|+|x+n|+|x+p|有最小值，其最小值是：|x﹣m|+|x+n|+|x+p|＝|﹣p﹣m|+|﹣p+n|+|﹣p+p|＝﹣p﹣m﹣n+p＝﹣m﹣n，

    则|x﹣m|+|x+n|+|x+p|的最小值是﹣m﹣n，

    故答案为：﹣m﹣n．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，E，F分别是正方形ABCD边AD、BC上的两定点，M是线段EF上的一点，过M的直线与正方形ABCD的边交于点P和点H，且PH=EF，则满足条件的直线PH最多有( )条

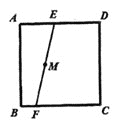
    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D．

    试说明：AC∥DF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一个长方体长，宽，高.从这个长方体的一个角上挖掉一个棱长的正方体，剩下部分的体积是（______），剩下部分的表面积是（______）.

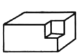
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果三角形有一边上的中线长恰好等于这条边的长，那么称这个三角形为“有趣三角形”，这条中线称为“有趣中线”.已知中，，一条直角边为3，如果是“有趣三角形”，那么这个三角形“有趣中线”的长等于________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

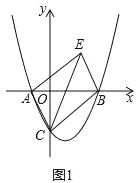
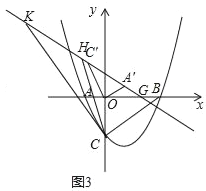
    【题目】如图1，在平面直角坐标系中，抛物线与x轴交于A、B两点（点A在点B左侧），与y轴交于C点，点E在第一象限且四边形ACBE为矩形．

    （1）求∠BCE的度数；

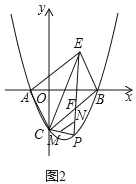
    （2）如图2，F为线段BC上一动点，P为第四象限内抛物线上一点，连接CP、FP、BP、EF，M，N分别是线段CP，FP的中点，连接MN，当△BCP面积最大，且MN+EF最小时，求PF的长度；

    （3）如图3，将△AOC绕点O顺时针旋转一个角度α（0°＜α＜180°），点A，C的对应点分别为A'，C'，直线A'C'与x轴交于点G，G在x轴正半轴上且OG=．线段KH在直线A'C'上平移（ K在H左边），且KH=5，△KHC是否能成为等腰三角形？若能，请求出所有符合条件的点K的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，己知抛物线y=k（x+1）（x﹣3k）（且k＞0）与x轴分别交于A、B两点，A点在B点左边，与Y轴交于C点，连接BC，过A点作AE∥CB交抛物线于E点，0为坐标原点．

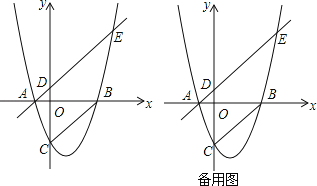
    （1）用k表示点C的坐标（0， ）；

    （2）若k=1，连接BE，

    ①求出点E的坐标；

    ②在x轴上找点P，使以P、B、C为顶点的三角形与△ABE相似，求出P点坐标；

    （3）若在直线AE上存在唯一的一点Q，连接OQ、BQ，使OQ⊥BQ，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数形结合是重要的数学思想方法之一，数形结合具体地说就是将抽象数学语言与直观图形结合起来，使抽象思维与形象思维结合起来，通过“数”与“形”之间的对应和转变来解决数学问题。数轴是数形结合的最基础图形，是连接数与形的桥梁之一，请解决下面的问题：

    （1）如图1，点B表示的数是1，则点A表示的数是 .

    （2）如果点M表示数－2，将点M向右移动6个单位长度到达终点N，那么终点N表示的数是4，此时M、N两点间的距离是 .

    （3）若∣x－0∣意义表示数x到原点的距离，则∣x－3∣的意义表示数x到3的距离；类似的式子∣x＋3∣=4，则x= .

    （4）由（3）可知，一般地，如果点A表示数为a，点B表示的数b，则A、B两点间的距离表示为 .

    （5）如图2，数轴上的两个点A、B所表示的数分别是a，b，点O为原点。在a＋b，a－b，∣a∣－∣b∣这三个运算结果中，是正数的有 个.

    （6）利用数轴直接写出∣x－2∣＋∣x＋5∣的最小值= .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，为坐标原点，矩形的顶点、，将矩形的一个角沿直线折叠，使得点落在对角线上的点处，折痕与轴交于点．

    （1）求线段的长度；

    （2）求直线所对应的函数表达式；

    （3）若点在线段上，在线段上是否存在点，使以为顶点的四边形是平行四边形？若存在，请求出点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案