
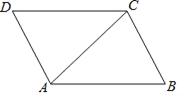
【题目】如图,AC是平行四边形ABCD的对角线.
(1)利用尺规作出AC的垂直平分线(要求保留作图痕迹,不写作法);
(2)设AC的垂直平分线分别与AB,AC,CD交于点E,O,F,求证:以A、E、C、F为顶点的四边形为菱形.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
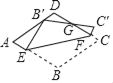
【题目】如图,在菱形紙片ABCD中,AB=2.将纸片折叠,使点B落在AD边上的点B′处(不与A,D重合),点C落在C′处,线段B′C′与直线CD交于点G,折痕为EF,则下列说法:①若∠A=90,B′为AD中点时,AE=![]() ;②若∠A=60°,B′为AD中点时,点E恰好是AB的中点;③若∠A=60°,C′F⊥CD时,
;②若∠A=60°,B′为AD中点时,点E恰好是AB的中点;③若∠A=60°,C′F⊥CD时,![]() ,其中正确的是( )
,其中正确的是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .一动点
.一动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 匀速运动,到达
匀速运动,到达![]() 点后,立即以原速度沿
点后,立即以原速度沿![]() 返回;另一动点
返回;另一动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 匀速运动,点
匀速运动,点![]() 、
、![]() 同时出发,当两点相遇时停止运动.在点
同时出发,当两点相遇时停止运动.在点![]() 、
、![]() 的运动过程中,以
的运动过程中,以![]() 为边作等边
为边作等边![]() ,使
,使![]() 和矩形
和矩形![]() 在射线
在射线![]() 的同侧,设运动的时间为
的同侧,设运动的时间为![]() 秒(
秒(![]() ).
).

(1)当等边![]() 的边
的边![]() 恰好经过点
恰好经过点![]() 时,求运动时间
时,求运动时间![]() 的值;
的值;
(2)在![]() 未到达
未到达![]() 的过程中,设等边
的过程中,设等边![]() 和矩形
和矩形![]() 重叠部分的面积为
重叠部分的面积为![]() ,请求出
,请求出![]() 与
与![]() 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
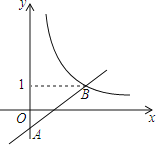
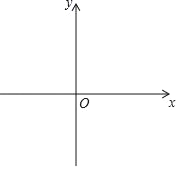
【题目】如图,在平面直角坐标系xOy中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A,与函数![]() (x>0)的图象相交于点B(t,1).
(x>0)的图象相交于点B(t,1).
(1)求点B的坐标及一次函数的解析式;
(2)点P的坐标为(m,m)(m>0),过P作PE∥x轴,交直线AB于点E,作PF∥y轴,交函数![]() (x>0)的图象于点F.
(x>0)的图象于点F.
①若m=2,比较线段PE,PF的大小;
②直接写出使PE≤PF的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
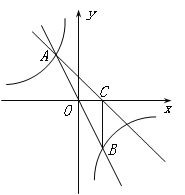
【题目】如图,在直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
(1)求m、n的值;
(2)求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣(a+1)x﹣3与x轴交于A、B两点,点A的坐标为(﹣1,0).
(1)求B点与顶点D的坐标;
(2)经过点B的直线l与y轴正半轴交于点M,S△ADM=5,求直线l的解析式;
(3)点P(t,0)为x轴上一动点,过点P作x轴的垂线m,将抛物线在直线m左侧的部分沿直线m对折,图象的其余部分保持不变,得到一个新图象G.请结合图象回答:当图象G与直线l没有公共点时,t的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
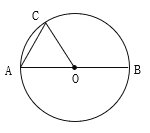
【题目】如图,在⊙O中,AB是直径,半径为R,弧AC=![]() R.
R.
求:(1)∠AOC的度数.(2)若D为劣弧BC上的一动点,且弦AD与半径OC交于E点.试探求△AEC≌△DEO时,D点的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划购买A型和B型课桌凳共200套,经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,,且购买4套A型和6套B型课桌凳共需1820元。
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳的![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是直角△ABC斜边上的中线,过点D作垂直于AB的直线交BC于点F,交AC的延长线于点E.
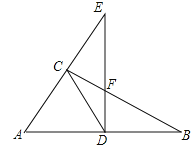
(1)求证:△ADE∽△FDB;
(2)若DF=2,EF=6,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com