
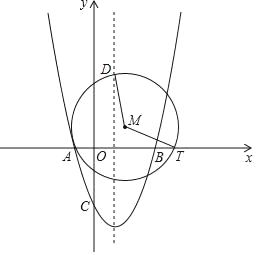
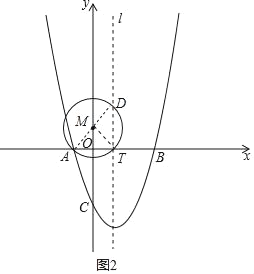
【题目】如图,二次函数y=x2+bx﹣3的图象与x轴分别相交于A、B两点,点B的坐标为(3,0),与y轴的交点为C,动点T在射线AB上运动,在抛物线的对称轴l上有一定点D,其纵坐标为2![]() ,l与x轴的交点为E,经过A、T、D三点作⊙M.
,l与x轴的交点为E,经过A、T、D三点作⊙M.
(1)求二次函数的表达式;
(2)在点T的运动过程中,
①∠DMT的度数是否为定值?若是,请求出该定值:若不是,请说明理由;
②若MT=![]() AD,求点M的坐标;
AD,求点M的坐标;
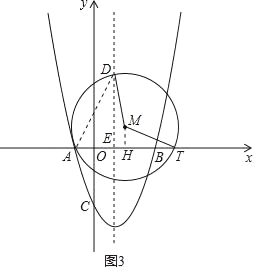
(3)当动点T在射线EB上运动时,过点M作MH⊥x轴于点H,设HT=a,当OH≤x≤OT时,求y的最大值与最小值(用含a的式子表示).
【答案】(1)y=x2﹣2x﹣3(2)①在点T的运动过程中,∠DMT的度数是定值②(0,![]() )(3)见解析
)(3)见解析
【解析】
(1)把点B的坐标代入抛物线解析式求得系数b的值即可;
(2)①如图1,连接AD.构造Rt△AED,由锐角三角函数的定义知,tan∠DAE=![]() .即∠DAE=60°,由圆周角定理推知∠DMT=2∠DAE=120°;
.即∠DAE=60°,由圆周角定理推知∠DMT=2∠DAE=120°;
②如图2,由已知条件MT=![]() AD,MT=MD,推知MD=
AD,MT=MD,推知MD=![]() AD,根据△ADT的外接圆圆心M在AD的中垂线上,得到:点M是线段AD的中点时,此时AD为⊙M的直径时,MD=
AD,根据△ADT的外接圆圆心M在AD的中垂线上,得到:点M是线段AD的中点时,此时AD为⊙M的直径时,MD=![]() AD.根据点A、D的坐标求得点M的坐标即可;
AD.根据点A、D的坐标求得点M的坐标即可;
(3)如图3,作MH⊥x于点H,则AH=HT=![]() AT.易得H(a﹣1,0),T(2a﹣1,0).由限制性条件OH≤x≤OT、动点T在射线EB上运动可以得到:0≤a﹣1≤x≤2a﹣1.
AT.易得H(a﹣1,0),T(2a﹣1,0).由限制性条件OH≤x≤OT、动点T在射线EB上运动可以得到:0≤a﹣1≤x≤2a﹣1.
需要分类讨论:(i)当![]() ,即
,即![]() ,根据抛物线的增减性求得y的极值.
,根据抛物线的增减性求得y的极值.
(ii)当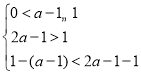 ,即
,即![]() <a≤2时,根据抛物线的增减性求得y的极值.
<a≤2时,根据抛物线的增减性求得y的极值.
(iii)当a﹣1>1,即a>2时,根据抛物线的增减性求得y的极值.
解:(1)把点B(3,0)代入y=x2+bx﹣3,得32+3b﹣3=0,
解得b=﹣2,
则该二次函数的解析式为:y=x2﹣2x﹣3;
(2)①∠DMT的度数是定值.理由如下:
如图1,连接AD.
∵抛物线y=x2﹣2x﹣3=(x﹣1)2﹣4.
∴抛物线的对称轴是直线x=1.
又∵点D的纵坐标为2![]() ,
,
∴D(1,2![]() ).
).
由y=x2﹣2x﹣3得到:y=(x﹣3)(x+1),
∴A(﹣1,0),B(3,0).
在Rt△AED中,tan∠DAE=![]() .
.
∴∠DAE=60°.
∴∠DMT=2∠DAE=120°.
∴在点T的运动过程中,∠DMT的度数是定值;
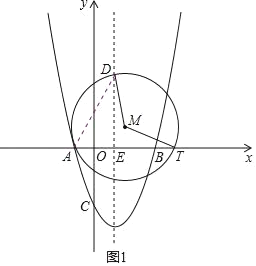
②如图2,∵MT=![]() AD.又MT=MD,
AD.又MT=MD,
∴MD=![]() AD.
AD.
∵△ADT的外接圆圆心M在AD的中垂线上,
∴点M是线段AD的中点时,此时AD为⊙M的直径时,MD=![]() AD.
AD.
∵A(﹣1,0),D(1,2![]() ),
),
∴点M的坐标是(0,![]() ).
).
(3)如图3,作MH⊥x于点H,则AH=HT=![]() AT.
AT.
又HT=a,
∴H(a﹣1,0),T(2a﹣1,0).
∵OH≤x≤OT,又动点T在射线EB上运动,
∴0≤a﹣1≤x≤2a﹣1.
∴0≤a﹣1≤2a﹣1.
∴a≥1,
∴2a﹣1≥1.
(i)当![]() ,即1
,即1![]() 时,
时,
当x=a﹣1时,y最大值=(a﹣1)2﹣2(a﹣1)﹣3=a2﹣4a;
当x=1时,y最小值=4.
(ii)当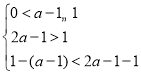 ,即
,即![]() <a≤2时,
<a≤2时,
当x=2a﹣1时,y最大值=(2a﹣1)2﹣2(2a﹣1)﹣3=4a2﹣8a.
当x=1时,y最小值=﹣4.
(iii)当a﹣1>1,即a>2时,
当x=2a﹣1时,y最大值=(2a﹣1)2﹣2(2a﹣1)﹣3=4a2﹣8a.
当x=a﹣1时,y最小值=(a﹣1)2﹣2(a﹣1)﹣3=a2﹣4a.


科目:初中数学 来源: 题型:
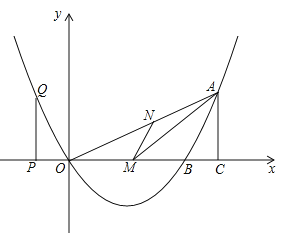
【题目】如图,已知二次函数的图象过点![]() .
.![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,且对称轴是直线
,且对称轴是直线![]() .
.
(1)求该二次函数的解析式;
(2)若![]() 是
是![]() 上的一点,作
上的一点,作![]() 交
交![]() 于
于![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的长;
的长;
(3)![]() 是
是![]() 轴上的点,过
轴上的点,过![]() 作
作![]() 轴与抛物线交于
轴与抛物线交于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,当以
,当以![]() 为顶点的三角形与以
为顶点的三角形与以![]() 为顶点的三角形相似时,求
为顶点的三角形相似时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=mx+n与双曲线y=![]() 相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.
相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.
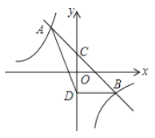
(1)求m,n的值;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)在坐标轴上是否存在异于D点的点P,使得S△PAB=S△DAB?若存在,直接写出P点坐标;若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC中,AB=4cm,以C为圆心,1cm长为半径画⊙C,点P在⊙C上运动,连接AP,并将AP绕点A顺时针旋转60°至AP′,点D是边AC的中点,连接DP′.在点P移动的过程中,线段DP′长度的最小值为______cm.
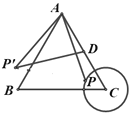
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佳佳调査了七年级400名学生到校的方式,根据调查结果绘制出统计图的一部分如图:
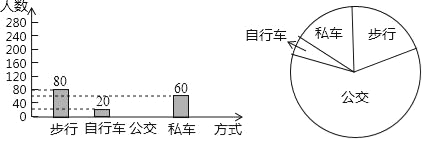
(1)补全条形统计图;
(2)求扇形统计图中表示“步行”的扇形圆心角的度数;
(3)估计在3000名学生中乘公交的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
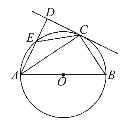
【题目】如图,已知AB是☉O的直径,DC是☉O的切线,点C是切点,AD⊥DC,垂足为D,且与圆O相交于点E.
(1)求证:∠DAC=∠BAC.
(2)若☉O的直径为5cm,EC=3cm,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
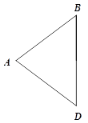
【题目】如图,在△ABD中,∠ABD = ∠ADB,分别以点B,D为圆心,AB长为半径在BD的右侧作弧,两弧交于点C,连接BC,DC和AC,AC与BD交于点O.
(1)用尺规补全图形,并证明四边形ABCD为菱形;
(2)如果AB = 5,![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com