
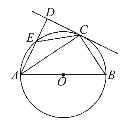
【题目】如图,已知AB是☉O的直径,DC是☉O的切线,点C是切点,AD⊥DC,垂足为D,且与圆O相交于点E.
(1)求证:∠DAC=∠BAC.
(2)若☉O的直径为5cm,EC=3cm,求AC的长.
科目:初中数学 来源: 题型:
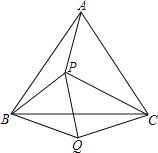
【题目】如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论中正确有_____(填序号)①△BPQ是等边三角形②△PCQ是直角三角形③∠APB=150° ④∠APC=120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇风力资源丰富,为了实现低碳环保,该乡镇决定开展风力发电,打算购买10台风力发电机组.现有A,B两种型号机组,其中A型机组价格为12万元/台,月均发电量为2.4万kw.h;B型机组价格为10万元/台,月均发电量为2万kw.h.经预算该乡镇用于购买风力发电机组的资金不高于105万元.
(1)请你为该乡镇设计几种购买方案;
(2)如果该乡镇用电量不低于20.4万kw.h/月,为了节省资金,应选择那种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①9a﹣3b+c=0;②4a﹣2b+c>0;③方程ax2+bx+c﹣4=0有两个相等的实数根;④方程a(x﹣1)2+b(x﹣1)+c=0的两根是x1=﹣2,x2=2.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )

A. 6B. 5C. 4D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
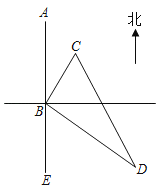
【题目】如图所示,幸福小区C位于快递站点B的北偏东35°方向,沁苑小区D位于B的南偏东55°方向,无人机以1千米/分钟的速度配送快递时,从B到C需飞行8分钟,从B到D需飞行15分钟.若无人机的配送路线是B→C→D→B请求出配送途中飞行所需时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N再分别以MN为圆心,大于
,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N再分别以MN为圆心,大于![]() 的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的有________.
的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的有________.
①AD是![]() 的平分线;②
的平分线;②![]() ;③点D在AB的中垂线上;④
;③点D在AB的中垂线上;④![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
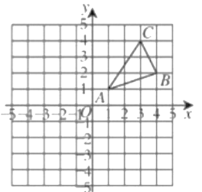
【题目】如图,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)若![]() 与
与![]() 关于
关于![]() 轴成轴对称,画出
轴成轴对称,画出![]() 的位置,
的位置,![]() 三个顶点坐标分别为
三个顶点坐标分别为![]() _______,
_______,![]() _________,
_________,![]() __________;
__________;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() ,如果存在,求出点
,如果存在,求出点![]() 的坐标,如果不存在,说明理由.
的坐标,如果不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com