
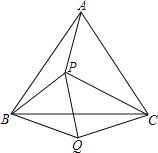
【题目】如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论中正确有_____(填序号)①△BPQ是等边三角形②△PCQ是直角三角形③∠APB=150° ④∠APC=120°
【答案】①②③
【解析】
①根据△ABC是等边三角形,得出∠ABC=60°,根据△BQC≌△BPA,得出∠CBQ=∠ABP,PB=QB=4,PA=QC=3,∠BPA=∠BQC,求出∠PBQ=60°,即可判断①;
②根据勾股定理的逆定理即可判断得出②;
③根据△BPQ是等边三角形,△PCQ是直角三角形即可判断;
④求出∠APC=150°﹣∠QPC,和PC≠2QC,可得∠QPC≠30°,即可判断④.
解:①∵△ABC是等边三角形,
∴∠ABC=60°,
∵△BQC≌△BPA,
∴∠CBQ=∠ABP,PB=QB=4,PA=QC=3,∠BPA=∠BQC,
∴∠PBQ=∠PBC+∠CBQ=∠PBC+∠ABP=∠ABC=60°,
∴△BPQ是等边三角形,
所以①正确;
②PQ=PB=4,
PQ2+QC2=42+32=25,
PC2=52=25,
∴PQ2+QC2=PC2,
∴∠PQC=90°,
∴△PCQ是直角三角形,
所以②正确;
③∵△BPQ是等边三角形,
∴∠PQB=∠BPQ=60°,
∴∠APB=∠BQC=∠BQP+∠PQC=60°+90°=150°,
所以③正确;
④∠APC=360°﹣150°﹣60°﹣∠QPC=150°﹣∠QPC,
∵∠PQC=90°,PC≠2QC,
∴∠QPC≠30°,
∴∠APC≠120°.
所以④错误.
所以正确的有①②③.
故答案为:①②③.


科目:初中数学 来源: 题型:
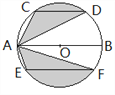
【题目】运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8。则图中阴影部分的面积是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一艘渔轮在海上C处作业时,发生故障,立即向搜救中心发出救援信号,此时搜救中心的两艘救助轮救助一号和救助二号分别位于海上A处和B处,B在A的正东方向,且相距100里,测得地点C在A的南偏东60,在B的南偏东30方向上,如图所示,若救助一号和救助二号的速度分别为40里/小时和30里/小时,问搜救中心应派那艘救助轮才能尽早赶到C处救援?(![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿折线
的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒.
秒.


备用图
(1)![]() ___________
___________![]() ;
;
(2)若点![]() 恰好在
恰好在![]() 的角平分线上,求此时
的角平分线上,求此时![]() 的值:
的值:
(3)在运动过程中,当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系 xOy 中,抛物线y=ax2+bx+c 上部分点的横、纵坐标间的对应值如表:

则下列结论正确的是( )
A. 抛物线的开口向下
B. 抛物线的顶点坐标为(2.5,﹣8.75)
C. 当 x>4 时,y 随 x 的增大而减小
D. 抛物线必经过定点(0,﹣5)
查看答案和解析>>
科目:初中数学 来源: 题型:
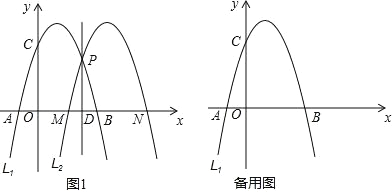
【题目】如图 1,已知抛物线 L1:y=﹣x2+2x+3 与 x 轴交于 A,B 两点(点 A在点 B 的左侧),与 y 轴交于点 C,在 L1 上任取一点 P,过点 P 作直线 l⊥x 轴, 垂足为D,将 L1 沿直线 l 翻折得到抛物线L2,交 x 轴于点 M,N(点 M 在点 N 的左侧).
(1)当 L1 与 L2 重合时,求点 P 的坐标;
(2)当点 P 与点 B 重合时,求此时 L2 的解析式;并直接写出 L1 与 L2 中,y 均随x 的增大而减小时的 x 的取值范围;
(3)连接 PM,PB,设点 P(m,n),当 n=![]() m 时,求△PMB 的面积.
m 时,求△PMB 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
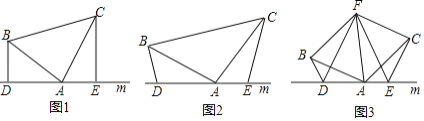
【题目】如图(1),已知:在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 直线
直线![]() ,
,![]() 直线
直线![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() .证明:
.证明:![]() .
.
(2)如图(2),将(1)中的条件改为:在![]() 中,
中,![]() ,
,![]() 、
、![]() 、
、![]() 三点都在直线
三点都在直线![]() 上,并且有
上,并且有![]() .请直接写出线段
.请直接写出线段![]() 、
、![]() 和
和![]() 之间的数量关系.
之间的数量关系.
(3)拓展与应用:如图(3),![]() 、
、![]() 是
是![]() 、
、![]() 、
、![]() 三点所在直线
三点所在直线![]() 上的两动点
上的两动点![]() 、
、![]() 、
、![]() 三点互不重合),点
三点互不重合),点![]() 为
为![]() 平分线上的一点,且
平分线上的一点,且![]() 和
和![]() 均为等边三角形,连接
均为等边三角形,连接![]() 、
、![]() ,若
,若![]() ,试证明
,试证明![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
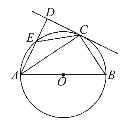
【题目】如图,已知AB是☉O的直径,DC是☉O的切线,点C是切点,AD⊥DC,垂足为D,且与圆O相交于点E.
(1)求证:∠DAC=∠BAC.
(2)若☉O的直径为5cm,EC=3cm,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com