
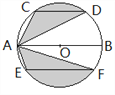
【题目】运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8。则图中阴影部分的面积是__________.
【答案】![]() π
π
【解析】分析:作直径CG,连接OD,OE,OF,DG,则根据圆周角定理求得DG的长,证明DG=EF,则S扇形ODG=S扇形OEF,然后根据三角形的面积公式证明S△OCD=S△ACD,S△OEF=S△AEF,则S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆,即可求解.

详解:作直径CG,连接OD,OE,OF,DG,
∵CG是圆的直径,
∴∠CDG=90°,则DG=![]() ,
,
又∵EF=8,
∴DG=EF,
∴弧DG=弧EF,
∴S扇形ODG=S扇形OEF,
∵AB∥CD∥EF,
∴S△OCD=S△ACD,S△OEF=S△AEF,
∴S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆![]() π×52=
π×52=![]() π,故答案为:
π,故答案为:![]() π.
π.
点睛:本题考查扇形面积的计算,圆周角定理,本题中找出两个阴影部分面积之间的联系是解题的关键.


科目:初中数学 来源: 题型:
【题目】(1)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点,且∠EAF=60°,请探究图中线段BE,EF,FD之间的数量关系是什么?
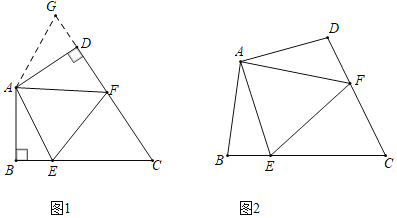
小明探究此问题的方法是:延长FD到点G,使DG=BE,连结AG.先证明△ABE≌△ADG,得AE=AG;再由条件可得∠EAF=∠GAF,证明△AEF≌△AGF,进而可得线段BE,EF,FD之间的数量关系是 .
(2)拓展应用:
如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD.问(1)中的线段BE,EF,FD之间的数量关系是否还成立?若成立,请给出证明;若不成立,请说明理由.
∠BAD.问(1)中的线段BE,EF,FD之间的数量关系是否还成立?若成立,请给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
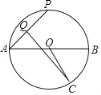
【题目】如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为( )
A. 3 B. 1+![]() C. 1+3
C. 1+3![]() D. 1+
D. 1+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市东湖高新技术开发区某科技公司,用480万元购得某种产品的生产技术后,并进一步投入资金1520万元购买生产设备,进行该产品的生产加工,已知生产这种产品每件还需成本费40元.经过市场调研发现:该产品的销售单价不低于100元,但不超过200元.设销售单价为x(元),年销售量为y(万件),年获利为w(万元)该产品年销售量y(万件)与产品售价x(元)之间的函数关系如图所示.
(1)直接写出y与x之间的函数关系式,并写出x的取值范围;
(2)求第一年的年获利w与x间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?并求当盈利最大或亏损最小时的产品售价;
(3)在(2)的条件下.即在盈利最大或亏损最小时,第二年公司重新确定产品售价,能否使两年共盈利不低于1370万元?若能,求出第二年的售价在什么范围内;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解本校学生对球类运动的爱好情况,采用抽样的方法,从乒乓球、羽毛球、篮球和排球四个方面调查了若干名学生,在还没有绘制成功的“折线统计图”与“扇形统计图”中,请你根据已提供的部分信息解答下列问题.

(1)在这次调查活动中,一共调查了 名学生,并请补全统计图.
(2)“羽毛球”所在的扇形的圆心角是 度.
(3)若该校有学生1200名,估计爱好乒乓球运动的约有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
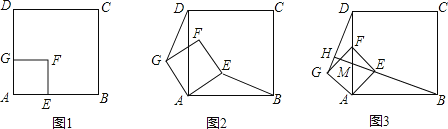
【题目】如图1,四边形ABCD,AEFG都是正方形,E、G分别在AB、AD边上,已知AB=4.
(1)求正方形ABCD的周长;
(2)将正方形AEFG绕点A逆时针旋转θ(0°<θ<90°)时,如图2,求证:BE=DG.
(3)将正方形AEFG绕点A逆时针旋转45°时,如图3,延长BE交DG于点H,设BH与AD的交点为M.
①求证:BH⊥DG;
②当AE=![]() 时,求线段BH的长(精确到0.1).
时,求线段BH的长(精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
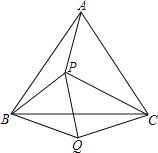
【题目】如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论中正确有_____(填序号)①△BPQ是等边三角形②△PCQ是直角三角形③∠APB=150° ④∠APC=120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com