
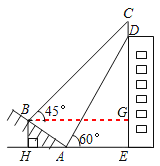
ЁОЬтФПЁПШчЭМЃЌФГДѓТЅЕФЖЅВПЪїгавЛПщЙуИцХЦCDЃЌаЁРюдкЩНЦТЕФЦТНХAДІВтЕУЙуИцХЦЕзВПDЕФбіНЧЮЊ60ЁуЃЎбиЦТУцABЯђЩЯзпЕНBДІВтЕУЙуИцХЦЖЅВПCЕФбіНЧЮЊ45ЁуЃЌвбжЊЩНЦТABЕФЦТЖШi=1ЃК![]() ЃЌAB=10УзЃЌAE=15УзЃЎЃЈi=1ЃК
ЃЌAB=10УзЃЌAE=15УзЃЎЃЈi=1ЃК![]() ЪЧжИЦТУцЕФЧІжБИпЖШBHгыЫЎЦНПэЖШAHЕФБШЃЉ
ЪЧжИЦТУцЕФЧІжБИпЖШBHгыЫЎЦНПэЖШAHЕФБШЃЉ

ЃЈ1ЃЉЧѓЕуBОрЫЎЦНУцAEЕФИпЖШBHЃЛ
ЃЈ2ЃЉЧѓЙуИцХЦCDЕФИпЖШЃЎ
ЃЈВтНЧЦїЕФИпЖШКіТдВЛМЦЃЌНсЙћОЋШЗЕН0.1УзЃЎВЮПМЪ§ОнЃК![]() 1.414ЃЌ
1.414ЃЌ![]() 1.732ЃЉ
1.732ЃЉ
ЁОД№АИЁПНтЃКЃЈ1ЃЉЙ§BзїBGЁЭDEгкGЃЌ
дкRtЁїABFжаЃЌi=tanЁЯBAH=![]() ЃЌЁрЁЯBAH=30Ёу
ЃЌЁрЁЯBAH=30Ёу
ЁрBH=![]() AB=5ЃЈУзЃЉЁЃ
AB=5ЃЈУзЃЉЁЃ
Д№ЃКЕуBОрЫЎЦНУцAEЕФИпЖШBHЮЊ5УзЁЃ
ЃЈ2ЃЉгЩЃЈ1ЃЉЕУЃКBH=5ЃЌAH=5![]() ЃЌ
ЃЌ
ЁрBG=AH+AE=5![]() +15ЁЃ
+15ЁЃ
дкRtЁїBGCжаЃЌЁЯCBG=45ЁуЃЌЁрCG=BG=5![]() +15ЁЃ
+15ЁЃ
дкRtЁїADEжаЃЌЁЯDAE=60ЁуЃЌAE=15ЃЌ
ЁрDE=![]() AE=15
AE=15![]() ЁЃ
ЁЃ
ЁрCD=CG+GEЉDE=5![]() +15+5Љ15
+15+5Љ15![]() =20Љ10
=20Љ10![]() Ёж2.7ЃЈУзЃЉЁЃ
Ёж2.7ЃЈУзЃЉЁЃ
Д№ЃКаћДЋХЦCDИпдМ2.7УзЁЃ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉЙ§BзїDEЕФДЙЯпЃЌЩшДЙзуЮЊGЃЎЗжБ№дкRtЁїABHжаЃЌЭЈЙ§НтжБНЧШ§НЧаЮЧѓГіBHЁЂAHЁЃ
ЃЈ2ЃЉдкЁїADEНтжБНЧШ§НЧаЮЧѓГіDEЕФГЄЃЌНјЖјПЩЧѓГіEHМДBGЕФГЄЃЌдкRtЁїCBGжаЃЌЁЯCBG=45ЁуЃЌдђCG=BGЃЌгЩДЫПЩЧѓГіCGЕФГЄШЛКѓИљОнCD=CG+GEЉDEМДПЩЧѓГіаћДЋХЦЕФИпЖШЁЃЁЁ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЪ§жсЩЯЯпЖЮABЃН2(ЕЅЮЛГЄЖШ)ЃЌЯпЖЮCDЃН4(ЕЅЮЛГЄЖШ)ЃЌЕуAдкЪ§жсЩЯБэЪОЕФЪ§ЪЧЃ10ЃЌЕуCдкЪ§жсЩЯБэЪОЕФЪ§ЪЧ16.ШєЯпЖЮABвдУПУы6ИіЕЅЮЛГЄЖШЕФЫйЖШЯђгвдШЫйдЫЖЏЃЌЭЌЪБЯпЖЮCDвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдШЫйдЫЖЏЃЎЩшдЫЖЏЪБМфЮЊt s.
(1)ЕБЕуBгыЕуCЯргіЪБЃЌЕуAЁЂЕуDдкЪ§жсЩЯБэЪОЕФЪ§ЗжБ№ЮЊ________ЃЛ
(2)ЕБtЮЊКЮжЕЪБЃЌЕуBИеКУгыЯпЖЮCDЕФжаЕужиКЯЃЛ
(3)ЕБдЫЖЏЕНBCЃН8(ЕЅЮЛГЄЖШ)ЪБЃЌЧѓГіДЫЪБЕуBдкЪ§жсЩЯБэЪОЕФЪ§ЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
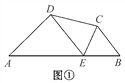
ЁОЬтФПЁПШчЭМЂй,дкЫФБпаЮABCDЕФБпABЩЯШЮШЁвЛЕуE(ЕуEВЛгыA,BжиКЯ),ЗжБ№СЌНгED,EC,ПЩвдАбЫФБпаЮABCDЗжГЩШ§ИіШ§НЧаЮ,ШчЙћЦфжагаСНИіШ§НЧаЮЯрЫЦ,ЮвУЧОЭАбEНазіЫФБпаЮABCDЕФБпABЩЯЕФЁАЯрЫЦЕуЁБ;ШчЙћетШ§ИіШ§НЧаЮЖМЯрЫЦ,ЮвУЧОЭАбEНазіЫФБпаЮABCDЕФБпABЩЯЕФЁАЧПЯрЫЦЕуЁБ.
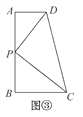
ЁОЪдЬтдйЯжЁПШчЭМЂк,дкЁїABCжа,ЁЯACB=90Ёу,жБНЧЖЅЕуCдкжБЯпDEЩЯ,ЗжБ№Й§ЕуA,BзїADЁЭDEгкЕуD,BEЁЭDEгкЕуE.ЧѓжЄ:ЁїADCЁзЁїCEB.
ЁОЮЪЬтЬНОПЁПдкЭМЂйжа,ШєЁЯA=ЁЯB=ЁЯDEC=40Ёу,ЪдХаЖЯЕуEЪЧЗёЪЧЫФБпаЮABCDЕФБпABЩЯЕФЯрЫЦЕу,ВЂЫЕУїРэгЩ.
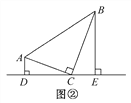
ЁОЩюШыЬНОПЁПШчЭМЂл,ADЁЮBC,DPЦНЗжЁЯADC,CPЦНЗжЁЯBCDНЛDPгкЕуP,Й§ЕуPзїABЁЭADгкЕуA,НЛBCгкЕуB.
(1)ЧыжЄУїЕуPЪЧЫФБпаЮABCDЕФБпABЩЯЕФвЛИіЧПЯрЫЦЕу.
(2)ШєAD=3,BC=5,ЪдЧѓABЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
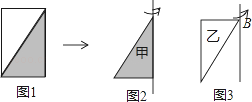
ЁОЬтФПЁПШчЭМ1ЃЌАбвЛеХГЄ10РхУзЁЂПэ6РхУзЕФГЄЗНаЮжНАхЗжГЩСНИіЯрЭЌЕФжБНЧШ§НЧаЮЃЎ
ЃЈ1ЃЉМзШ§НЧаЮЃЈШчЭМ2ЃЉа§зЊвЛжмЃЌПЩвдаЮГЩвЛИідѕбљЕФМИКЮЬхЃПЫќЕФЬхЛ§ЪЧЖрЩйСЂЗНУзЃП
ЃЈ2ЃЉввШ§НЧаЮЃЈШчЭМ3ЃЉа§зЊвЛжмЃЌПЩвдаЮГЩвЛИідѕбљЕФМИКЮЬхЃПЫќЕФЬхЛ§ЪЧЖрЩйСЂЗНУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкФГЕиЃЌШЫУЧЗЂЯждквЛЖЈЮТЖШЯТФГжжѓЌѓАНаЕФДЮЪ§гыЮТЖШжЎМфгаШчЯТЕФНќЫЦЙиЯЕЃКгУѓЌѓА1minНаЕФДЮЪ§Г§вд7ЃЌШЛКѓдйМгЩЯ3ЃЌОЭНќЫЦЕиЕУЕНИУЕиЕБЪБЕФЮТЖШЃЈЁцЃЉЃЎ
ЃЈ1ЃЉгУДњЪ§ЪНБэЪОИУЕиЕБЪБЕФЮТЖШЃЛ
ЃЈ2ЃЉЕБѓЌѓА1minНаЕФДЮЪ§ЗжБ№ЪЧ84ЃЌ105КЭ126ЪБЃЌИУЕиЕБЪБЕФЮТЖШдМЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЪ§жсЩЯ![]() ЕуБэЪОЪ§
ЕуБэЪОЪ§![]() ЃЌ
ЃЌ![]() ЕуБэЪОЪ§
ЕуБэЪОЪ§![]() ЃЌ
ЃЌ![]() БэЪО
БэЪО![]() ЕуКЭ
ЕуКЭ![]() ЕужЎМфЕФОрРыЃЌЧв
ЕужЎМфЕФОрРыЃЌЧв![]() ЁЂ
ЁЂ![]() Тњзу
Тњзу![]() Ъ§жсЩЯгавЛЖЏЕу
Ъ§жсЩЯгавЛЖЏЕу![]() ЃЌДг
ЃЌДг![]() ЕуГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђгвдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ
ЕуГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђгвдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ![]() Уы
Уы![]() ЃЌ
ЃЌ
![]()
ЃЈ1ЃЉЕу![]() БэЪОЕФЪ§ЮЊЁЁ ЁЁЃЌЕу
БэЪОЕФЪ§ЮЊЁЁ ЁЁЃЌЕу![]() БэЪОЕФЪ§ЮЊЁЁ ЁЁЃЎ
БэЪОЕФЪ§ЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉЕу![]() БэЪОЕФЪ§ЁЁ ЁЁЃЈгУКЌ
БэЪОЕФЪ§ЁЁ ЁЁЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ3ЃЉЕБЕу![]() дЫЖЏЁЁ ЁЁУыЪБЃЌЕу
дЫЖЏЁЁ ЁЁУыЪБЃЌЕу![]() КЭЕу
КЭЕу![]() жЎМфОрРыЮЊ4ЃЛ
жЎМфОрРыЮЊ4ЃЛ
ЃЈ4ЃЉШєЪ§жсЩЯСэгавЛЖЏЕу![]() ЃЌЭЌЪБДг
ЃЌЭЌЪБДг![]() ЕуГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђзѓдШЫйдЫЖЏЃЌЕБЕу
ЕуГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђзѓдШЫйдЫЖЏЃЌЕБЕу![]() КЭЕу
КЭЕу![]() жЎМфОрРыЮЊ6ЪБЃЌЧѓЪБМф
жЎМфОрРыЮЊ6ЪБЃЌЧѓЪБМф![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ 1ЃЌЖўДЮКЏЪ§![]() ЕФЭМЯёЙ§Еу A ЃЈ3ЃЌ0ЃЉЃЌB ЃЈ0ЃЌ4ЃЉСНЕуЃЌЖЏЕу P Дг A ГіЗЂЃЌдкЯпЖЮ AB ЩЯби A Ёњ B ЕФЗНЯђвдУПУы 2 ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЙ§ЕуPзї PDЁЭy гкЕу D ЃЌНЛХзЮяЯпгкЕу C ЃЎЩшдЫЖЏЪБМфЮЊ t ЃЈУыЃЉЃЎ
ЕФЭМЯёЙ§Еу A ЃЈ3ЃЌ0ЃЉЃЌB ЃЈ0ЃЌ4ЃЉСНЕуЃЌЖЏЕу P Дг A ГіЗЂЃЌдкЯпЖЮ AB ЩЯби A Ёњ B ЕФЗНЯђвдУПУы 2 ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЙ§ЕуPзї PDЁЭy гкЕу D ЃЌНЛХзЮяЯпгкЕу C ЃЎЩшдЫЖЏЪБМфЮЊ t ЃЈУыЃЉЃЎ
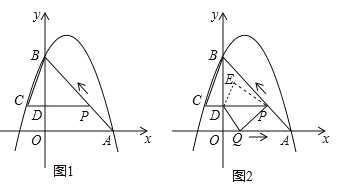
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
ЃЈ2ЃЉСЌНг BC ЃЌЕБtЃН![]() ЪБЃЌЧѓЁїBCPЕФУцЛ§ЃЛ
ЪБЃЌЧѓЁїBCPЕФУцЛ§ЃЛ
ЃЈ3ЃЉШчЭМ 2ЃЌЖЏЕу P Дг A ГіЗЂЪБЃЌЖЏЕу Q ЭЌЪБДг O ГіЗЂЃЌдкЯпЖЮ OA ЩЯби OЁњA ЕФЗНЯђвд 1ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЕБЕу P гы B жиКЯЪБЃЌP ЁЂ Q СНЕуЭЌЪБЭЃжЙдЫЖЏЃЌСЌНг DQ ЁЂ PQ ЃЌНЋЁїDPQбижБЯп PC елЕўЕН ЁїDPE ЃЎдкдЫЖЏЙ§ГЬжаЃЌЩш ЁїDPE КЭ ЁїOABжиКЯВПЗжЕФУцЛ§ЮЊ S ЃЌжБНгаДГі S гы t ЕФКЏЪ§ЙиЯЕЪНМА t ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЁїABCжаЃЌDЪЧBCБпЩЯвЛЕуЃЌЁЯ1=ЁЯ2ЃЌЁЯ3=ЁЯ4.
ЃЈ1ЃЉШєЁЯ1=35ЁуЃЌЧѓЁЯDACЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєЁЯBAC=69ЁуЃЌЧѓЁЯDACЕФЖШЪ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГізтГЕЫОЛњДгЙЋЫОГіЗЂЃЌдкЖЋЮїЗНЯђЕФШЫУёТЗЩЯСЌајНгЫЭ![]() ХњПЭШЫЃЌааЪЛТЗГЬМЧТМШчЯТ(ЙцЖЈЯђЖЋЮЊе§ЃЌЯђЮїЮЊИКЃЌЕЅЮЛ:
ХњПЭШЫЃЌааЪЛТЗГЬМЧТМШчЯТ(ЙцЖЈЯђЖЋЮЊе§ЃЌЯђЮїЮЊИКЃЌЕЅЮЛ:![]() ):
):
Ек | Ек | Ек | Ек | Ек |
|
|
|
|
|
ЃЈ1ЃЉНгЫЭЭъЕк![]() ХњПЭШЫКѓЃЌИУМнЪЛдБдкЙЋЫОЪВУДЗНЯђЃЌОрРыЙЋЫОЖрЩйЧЇУз?
ХњПЭШЫКѓЃЌИУМнЪЛдБдкЙЋЫОЪВУДЗНЯђЃЌОрРыЙЋЫОЖрЩйЧЇУз?
ЃЈ2ЃЉШєИУГізтГЕУПЧЇУзКФгЭ![]() Щ§ЃЌФЧУДдкетЙ§ГЬжаЙВКФгЭЖрЩйЩ§?
Щ§ЃЌФЧУДдкетЙ§ГЬжаЙВКФгЭЖрЩйЩ§?
ЃЈ3ЃЉШєИУГізтГЕЕФМЦМлБъзМЮЊЃКааЪЛТЗГЬВЛГЌЙ§![]() ЪеЗб
ЪеЗб![]() дЊЃЌГЌЙ§
дЊЃЌГЌЙ§![]() ЕФВПЗжАДУПЧЇУз
ЕФВПЗжАДУПЧЇУз![]() дЊЪеЗбЃЌдкетЙ§ГЬжаИУМнЪЛдБЙВЪеЕНГЕЗбЖрЩйдЊ?
дЊЪеЗбЃЌдкетЙ§ГЬжаИУМнЪЛдБЙВЪеЕНГЕЗбЖрЩйдЊ?
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com